Optimization and Dynamics

The study of dynamical systems began by trying to understand the relationship between the earth and the sun. Since the birth of calculus and modern computing, the study of optimization and dynamics have exploded, bringing new mathematical perspectives to disciplines previously unknown. Both optimization and dynamics continue to be important fields of research in disciplines such as mathematics, physics, engineering, biology, chemistry, and economics.

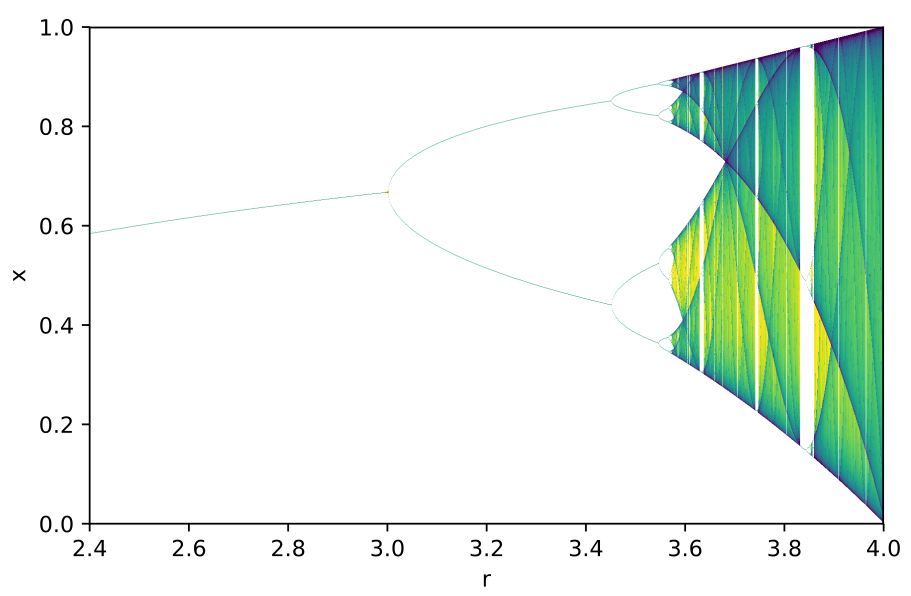
The bifurcation diagram of population growth.

We are using Zoom to meet and discuss virtually. We have two different Meeting IDs: one for Tuesday and one for Friday.

• Tuesday: 939-8199-5044
• Friday: 967-2582-7899

Documents

• Lecture Notes
• Tentative Schedule
• Course Information

---

Problem Sheets

Weekly exercise sheets are to be turned in electronically to your tutor, Dr. Lee. Unless stated otherwise, they are due Wednesdays by 23:59 (GMT+2).

• Problem set 1
• Problem set 2
• Problem set 3
• Problem set 4
• Problem set 5
• Problem set 6
• Problem set 7
• Problem set 8
• Problem set 9
• Problem set 10
• Problem set 11
• Problem set 12

---

Videos

Links to videos (on YouTube) where you can find videos on topics we discuss in the course. These follow the course lecture notes.

Chapter 8

• Basics of matrix exponentials
  • We look at the fundamentals of matrix exponentials. We define the expression $e^A$, or $\mathrm{exp}(A)$, and discuss how it comes up in the study of continuous time dynamical systems.
  • Notes
• Properties of matrix exponentials
  • We look at some basic properties of the matrix exponential, and we use them to compute more exponentials of more complicated matrices.
  • Notes
• Using characteristic polynomials to compute exponentials
  • This is the first video in a two part series where we use the characteristic polynomial of a matrix A to compute the exponential of A. We prove the propositions needed to apply this to matrix exponentials.
  • Notes
• Examples involving characteristic polynomials
  • This is the second video in the two part series on using the characteristic polynomial to compute the exponential of a matrix. Here, we apply the propositions that we proved in the first part in a few examples.
  • Notes
• Analysis of linear ODE systems Part 1
  • We take everything we have done in chapter 8 and use it to analyze linear systems of ODEs. We give a proof of the existence and uniqueness of solutions.
  • Notes
• Analysis of linear ODE systems Part 2
  • We take everything we have done in chapter 8 and use it to analyze linear systems of ODEs. We give an alternative description of a general solution to a linear ODE system, and we discuss various examples.
  • Notes

Chapter 9

• Basics of nonlinear stability
  • We look at stability properties of nonlinear continuous time systems based on the values of eigenvalues of the system, and we consider a few examples.
  • Notes
• Definition and examples of Lyapunov functions
  • We give the definition of a Lyapunov function with respect to an autonomous system, and we apply it to an example. We defer explaining the implications of the existence of a Lyapunov function to the behavior of the system.
  • Notes
• Lyapunov functions imply stability
  • We prove that the existence of a Lyapunov function in a neighborhood about a fixed point implies that the fixed point is stable.
  • Notes
• Strict Lyapunov functions imply more
  • We prove that strict Lyapunov functions on a neighborhood about a fixed point imply that the fixed point is asymptotically stable.
  • Notes
• Stability with Lyapunov functions
  • We look at applications of previous propositions concerning Lyapunov functions and the stability of fixed points. We discuss a general suite of potential Lyapunov functions for examples.
  • Notes
• Instability and a Lypaunov analog
  • We prove a Lyapunov analog for unstable fixed points. This is another tool we can use to show that a fixed point is unstable.
  • Notes
• Examples with unstable fixed points
  • After proving Prop. 9.13, we apply it to two examples, where we prove that a fixed point is unstable.
  • Notes

---

Handwritten notes

PDFs of the handwritten notes made during the lecture may be uploaded.

• Lecture 1
• Lecture 2
• Lecture 3
• Lecture 4
• Lecture 5
• Lecture 6
• Lecture 7
• Lecture 8
• Lecture 9
• Lecture 10
• Lecture 11
• Lecture 12
• Lecture 13
• Lecture 14
• Lecture 15
• Lecture 16
• Lecture 17
• Lecture 18
• Lecture 19

---

References

1. Arrowsmith, D. K.; Place, C. M. An introduction to dynamical systems. Cambridge University Press, Cambridge, 1990.
2. Devaney, Robert L. An introduction to chaotic dynamical systems. Second edition. Addison-Wesley Studies in Nonlinearity. Addison-Wesley Publishing Company, Advanced Book Program, Redwood City, CA, 1989.
3. Stokey, Nancy L., Lucas, Robert E., Jr. Recursive methods in economic dynamics. With the collaboration of Edward C. Prescott. Harvard University Press, Cambridge, MA, 1989.
4. Strogatz, Steven H. Nonlinear dynamics and chaos. With applications to physics, biology, chemistry, and engineering. Second edition. Westview Press, Boulder, CO, 2015.
5. Teschl, Gerald. Ordinary differential equations and dynamical systems. Graduate Studies in Mathematics, 140. American Mathematical Society, Providence, RI, 2012.

---