Isomorphism

We provide two functions dealing with isomorphisms of $E$-groups. One for deciding isomorphism between two $E$-groups, and the other for constructing a generating set for the automorphism group of such groups. These algorithms are based on (Theorem E) Maglione–Stanojkovski.

EGAutomorphismGroup

Input:

• GrpPC $G$.

Output:

• GrpAuto $A$.

Return $A=\mathrm{Aut}(G)$ provided $G$ is an $E$-group.

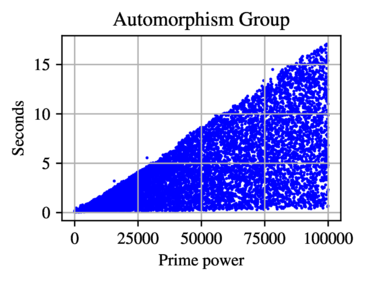
As we record in Maglione–Stanojkovski, the theoretical performance of EGAutomorphismGroup is $O(|G|^{1/9})$, and the actual performance can be observed in the following scatter plot of data.

EGIsIsomorphic

Input:

• GrpPC $G$,
• GrpPC $H$.

Output:

• BoolElt,
• Map $\varphi$.

Decide if $G$ and $H$ are $E$-groups and if $G\cong H$, and if so return an isomorphism $\varphi : G \to H$.