Symplectic Hecke eigenbases from Ehrhart polynomials

joshmaglione.com/spp25

Joshua Maglione

How to Navigate:

Spacebar: Forward

Shift + Spacebar: Backward

Escape: Jump around

Arrow keys: Move around

Creative Commons Attribution 4.0

International License

Claudia Alfes

Bielefeld

Christopher Voll

Bielefeld

Ehrhart polynomials

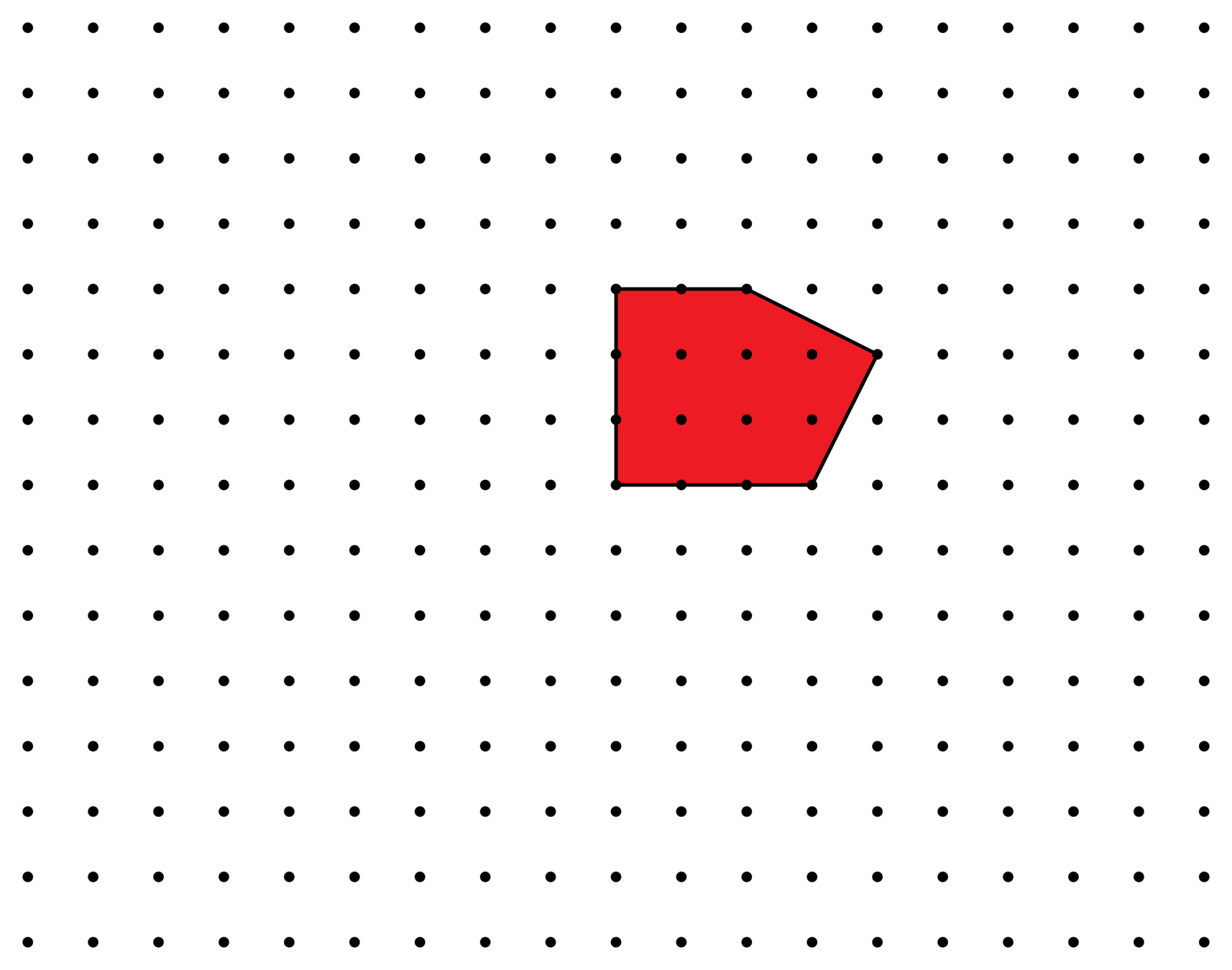
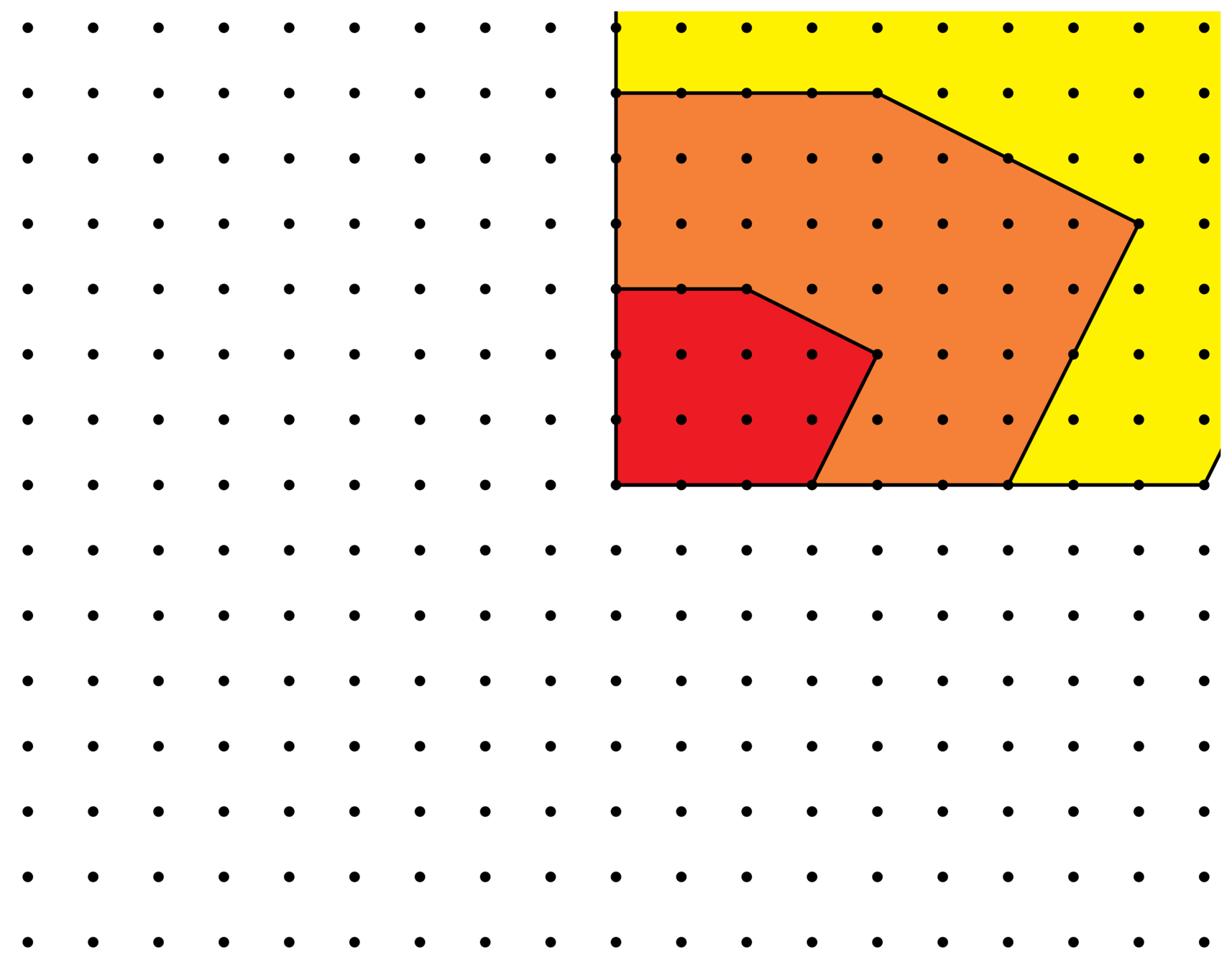
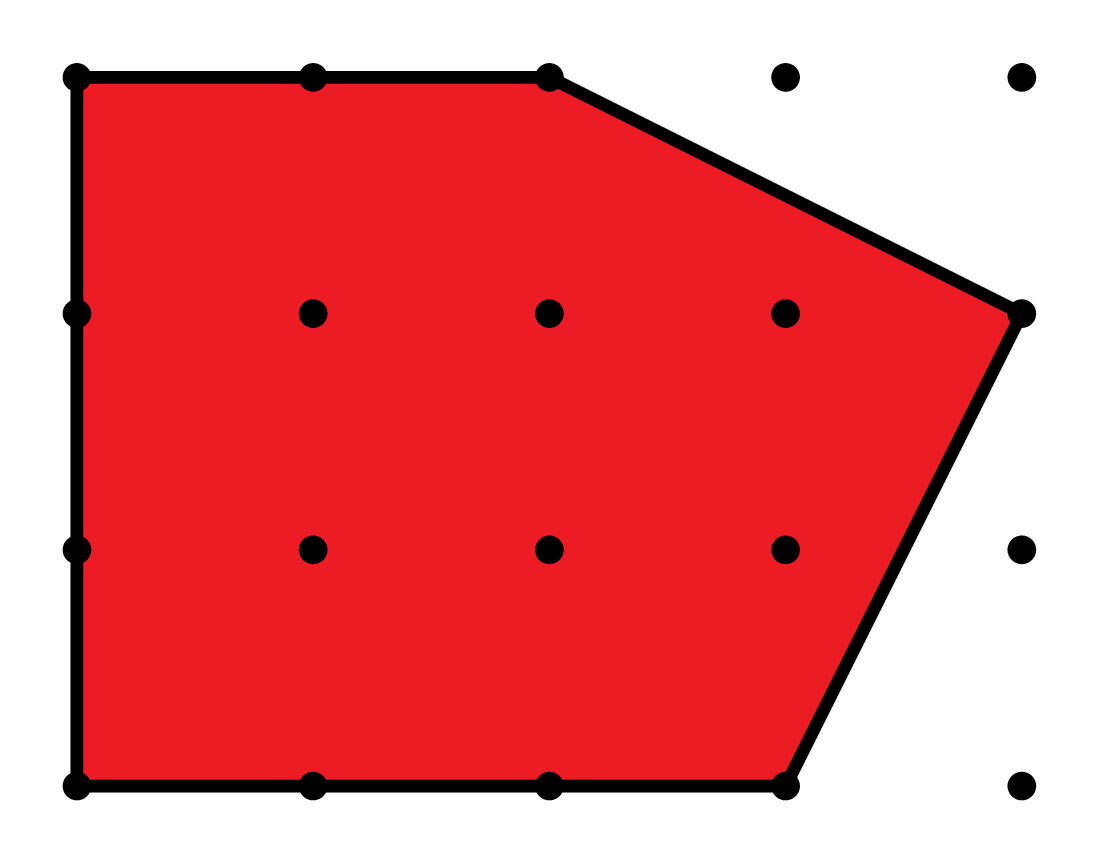
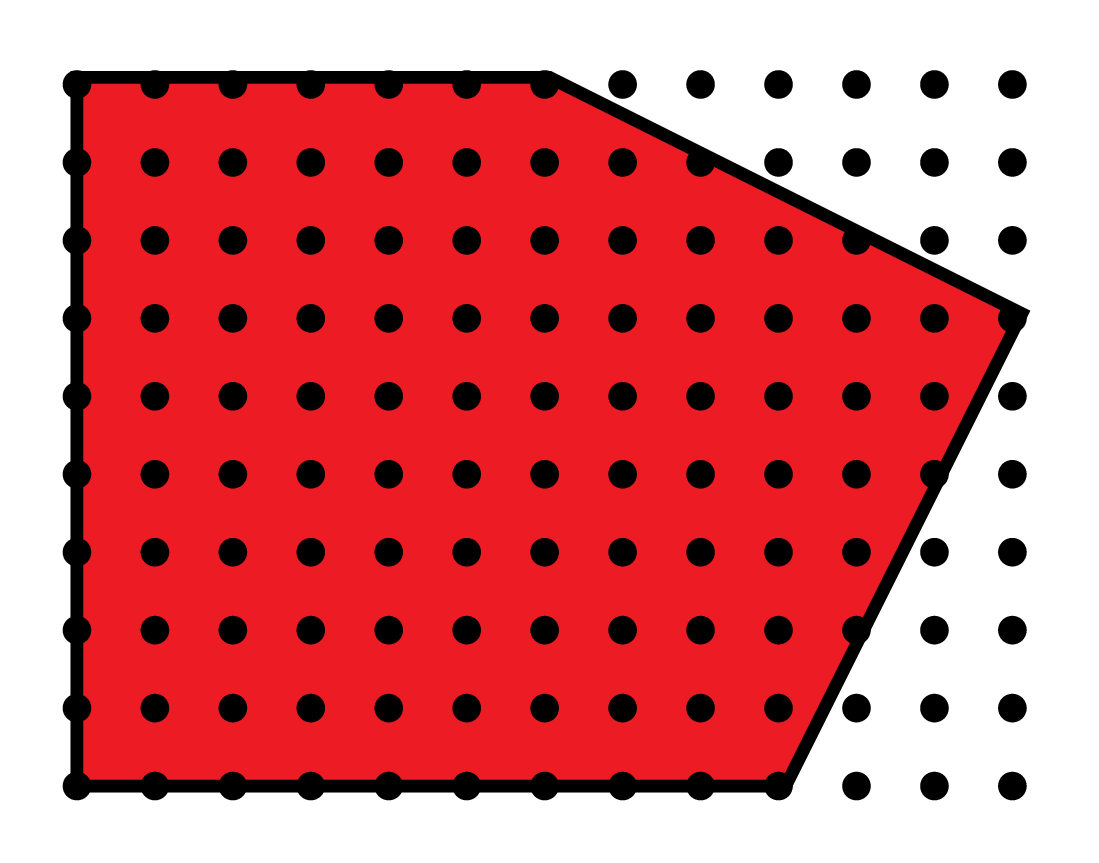
$E(t) = 10t^2 + 5t + 1$

$E_P^{\Lambda}(t)$ : Ehrhart polynomial

$t \mapsto \#(tP\cap \Lambda)$

lattice

polytope

$E(1)=16$

$E(3)=106$

$E(2)=51$

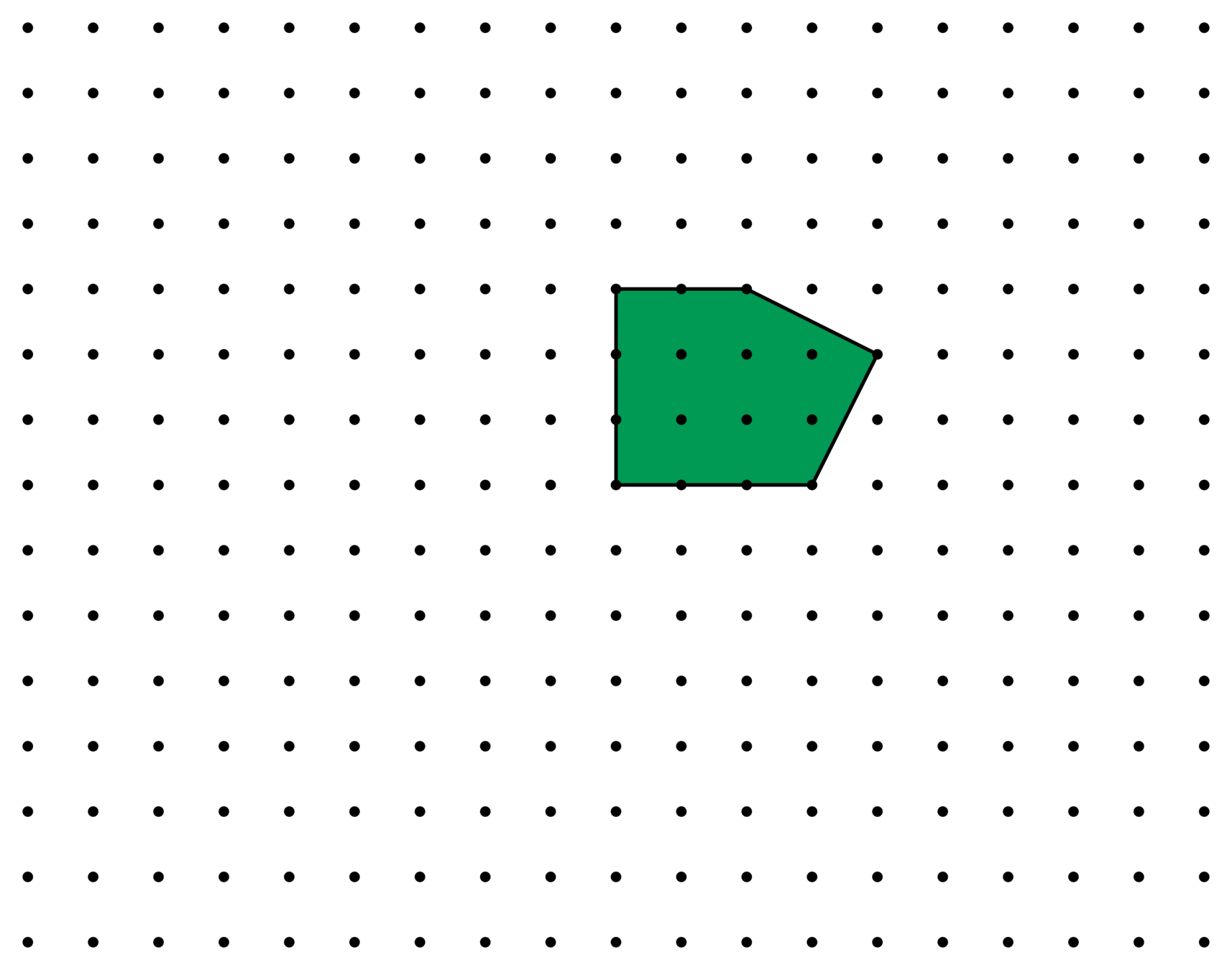
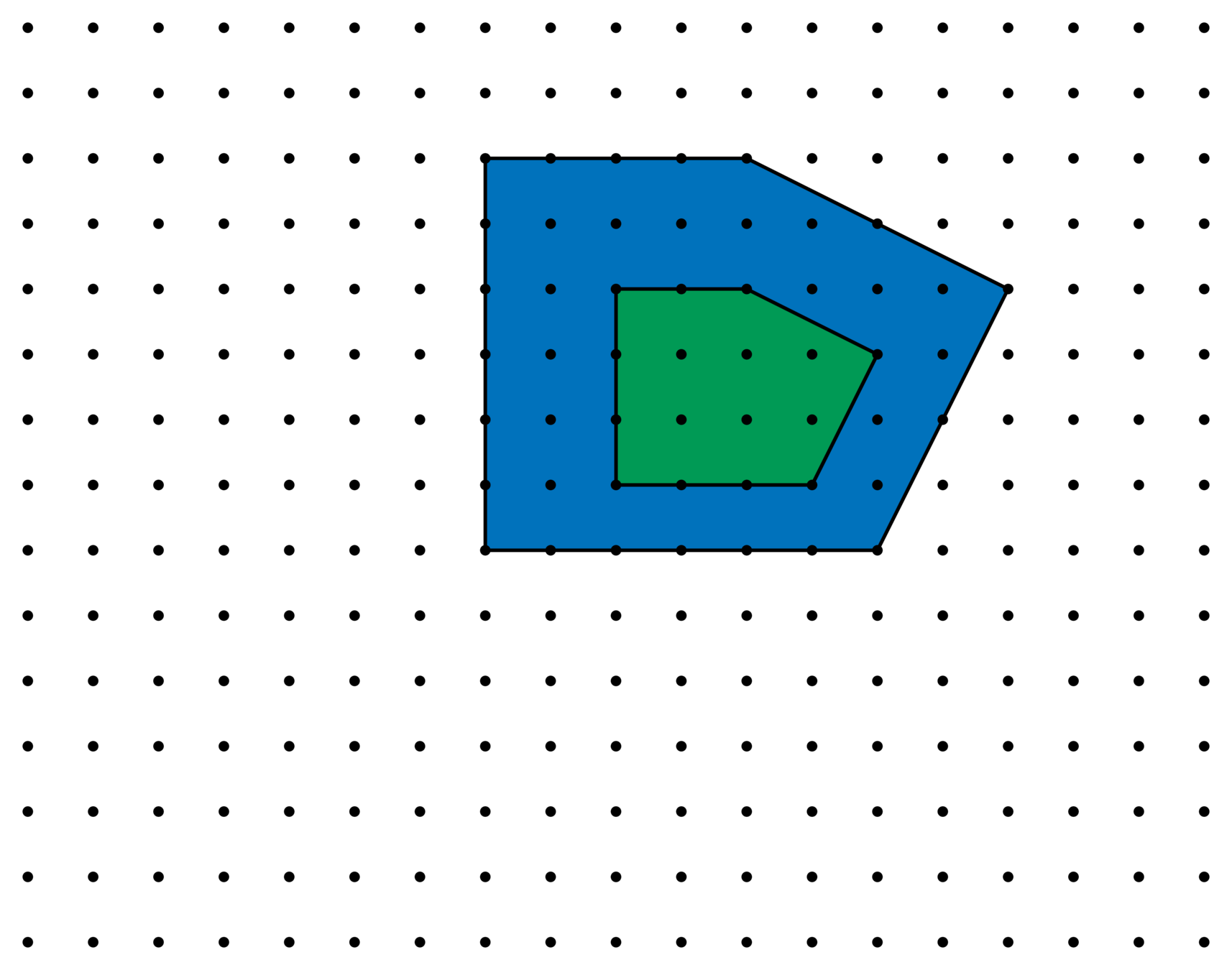
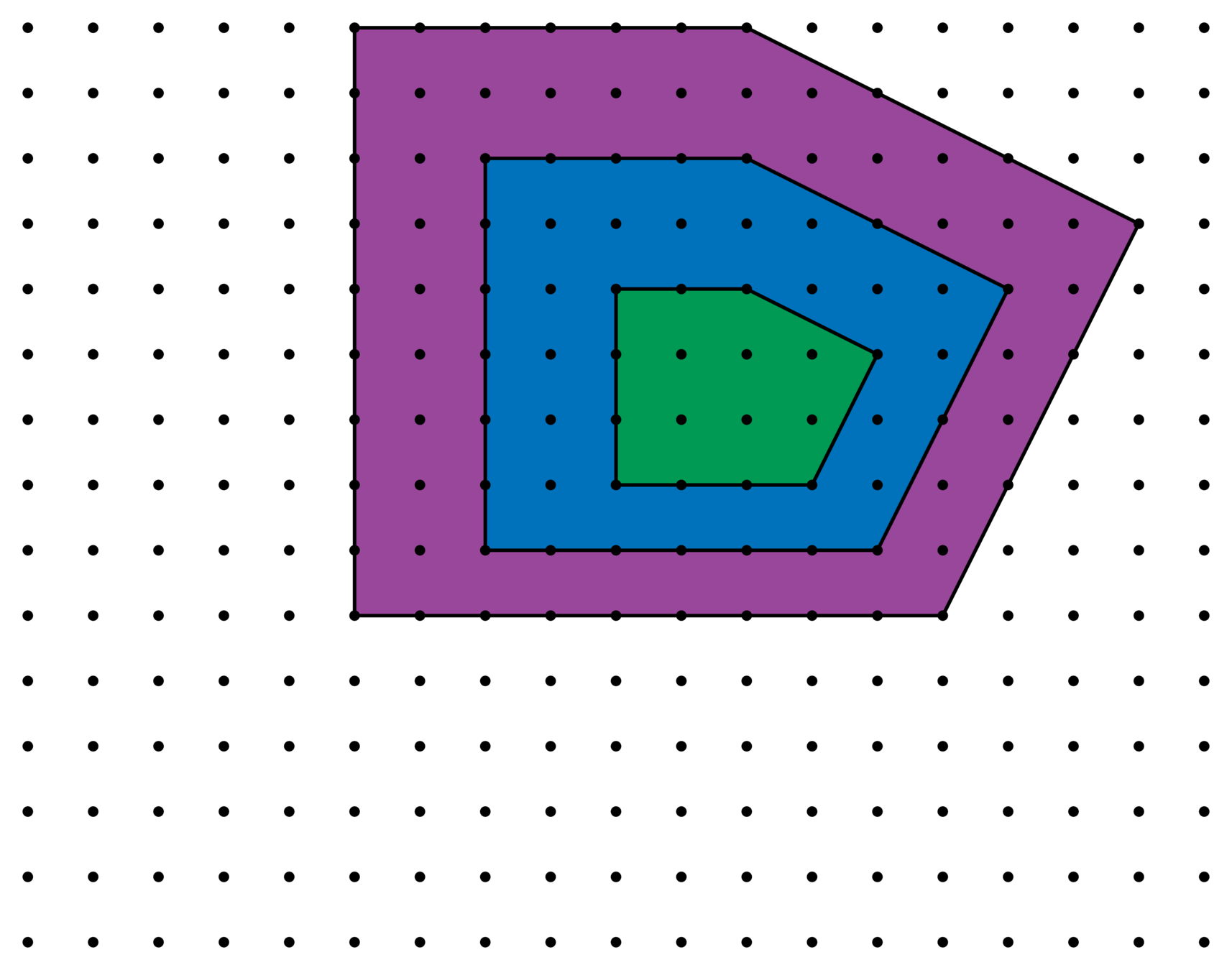
Lattices

$\Lambda$

$\frac{1}{2}\Lambda$

$\frac{1}{3}\Lambda$

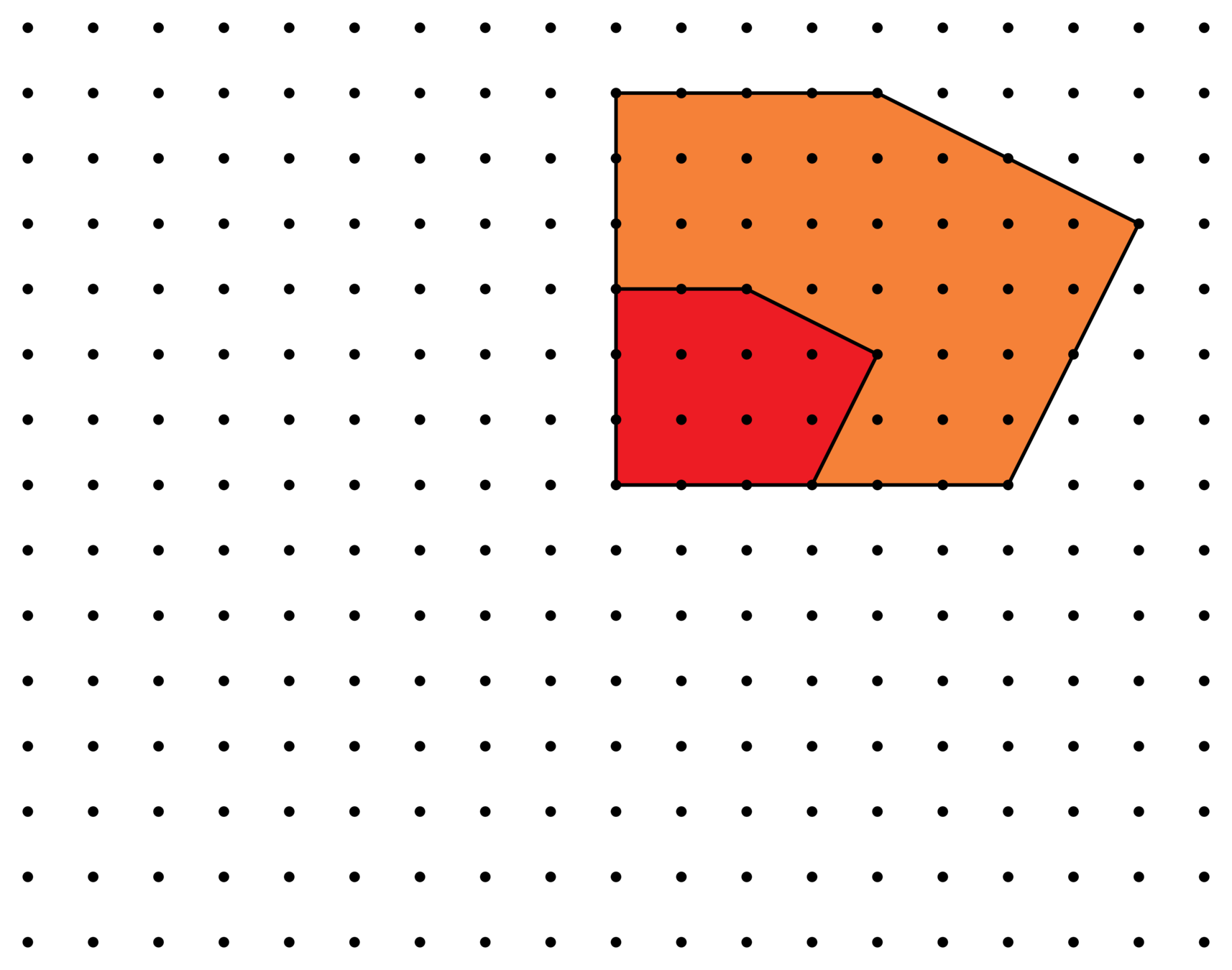
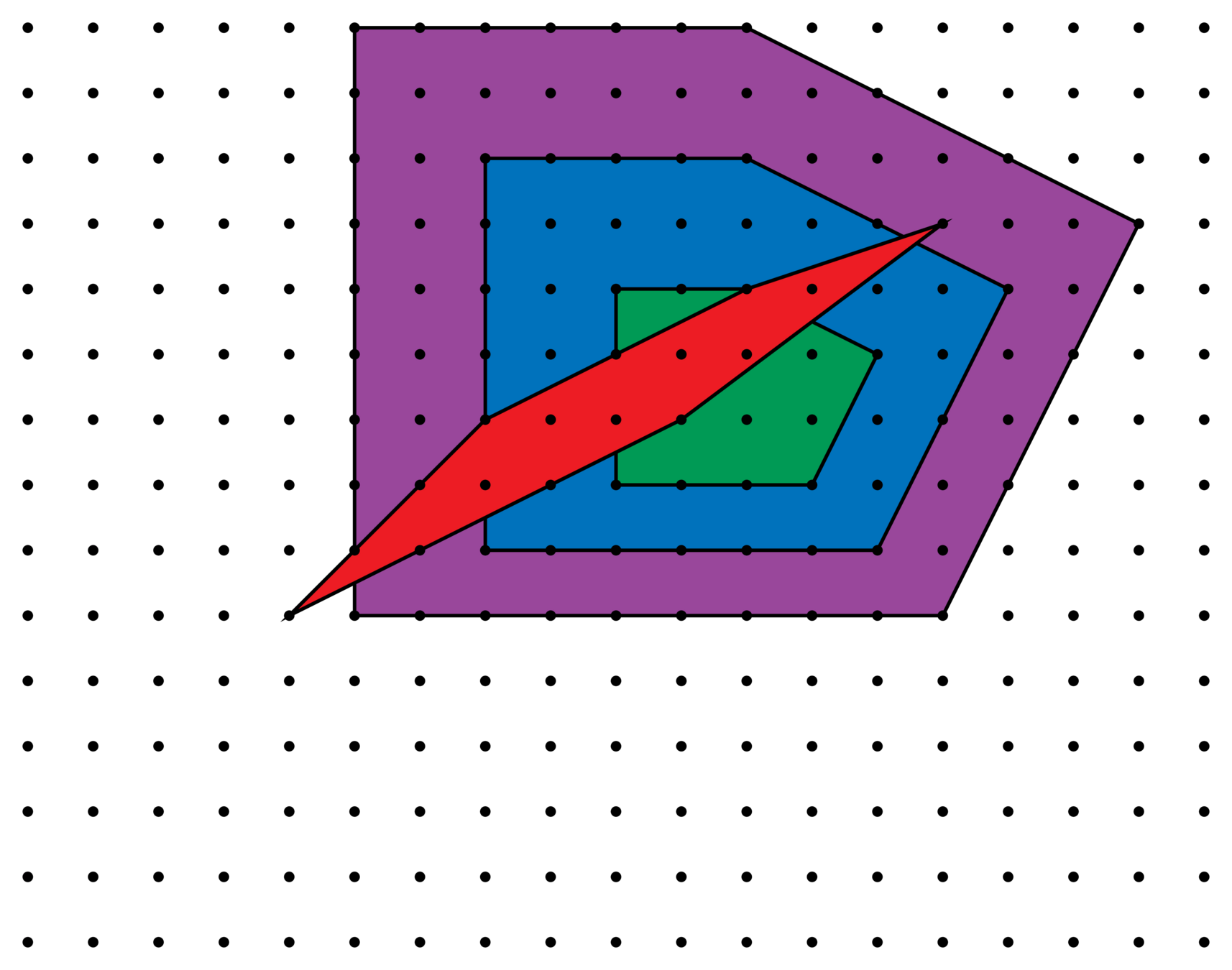
Consider how $\mathscr{E}_{n,\ell}^{\Lambda}$ changes as we refine the lattice $\Lambda$.

Let $E_P^{\Lambda}(t) = c_0 + c_1t + \cdots + c_nt^n$. For $\ell\in \{0,\dots, n\}=[n]_0$, define

\mathscr{E}_{n, \ell}^{\Lambda}(P) = c_{\ell}.

Thus, $\mathscr{E}_{n,\ell}^{\Lambda}$ is the function on polytopes in $\mathbb{R}^n$ extracting the $\ell$th coefficient of its Ehrhart polynomial.

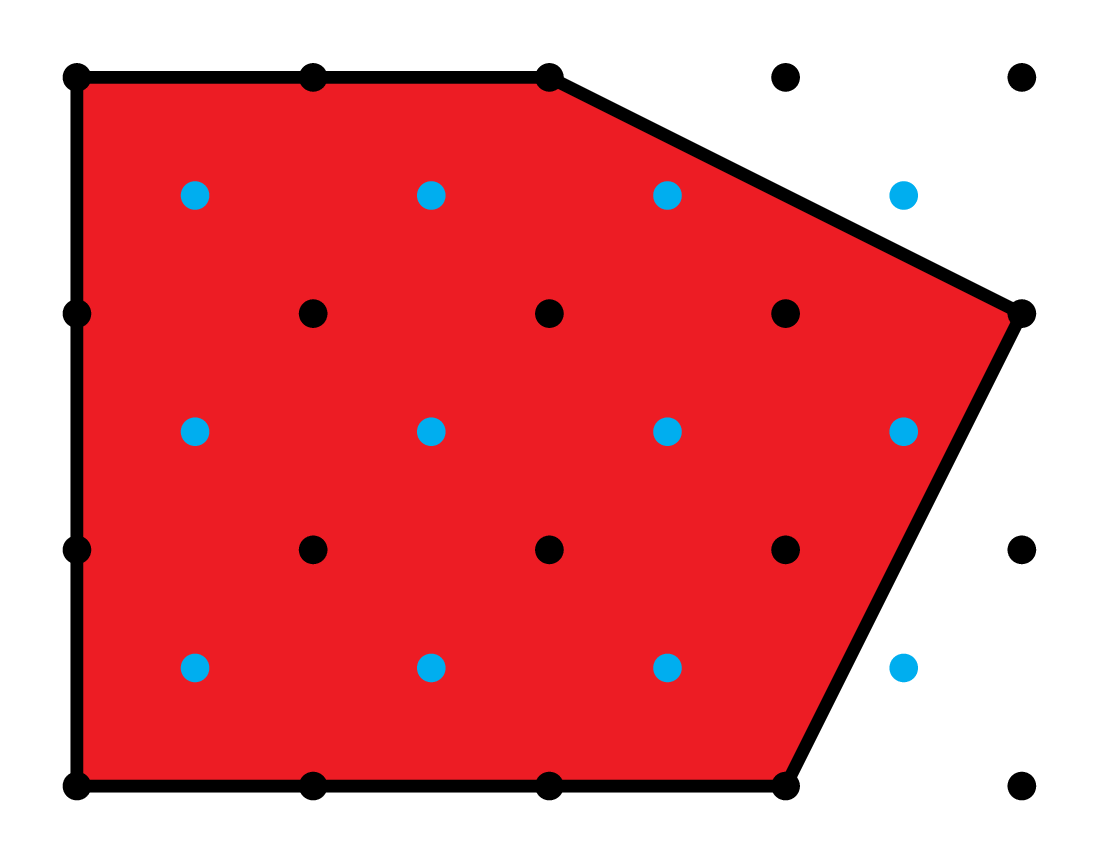
Lattices $\Lambda\supseteq\mathbb{Z}^2$

\Lambda = 2^{-1}\left(\begin{smallmatrix} \phantom{0} & \phantom{0} \\ \phantom{0} & \phantom{0} \end{smallmatrix}\right)

\Lambda = 4^{-1}\left(\begin{smallmatrix} \phantom{0} & \phantom{0} \\ \phantom{0} & \phantom{0} \end{smallmatrix}\right)

\mathcal{E}_{2, 1}^{\Lambda}(\phantom{poly})

\begin{aligned} \mathrm{conv}&\{(0,0), (0,3), (2,3),\\ &\;(3,0), (4,2)\} \end{aligned}

\begin{aligned} \mathrm{conv}&\{(0,0), (0,2), (1,4),\\ &\;(3,2), (4,0)\} \end{aligned}

\begin{aligned} \mathrm{conv}&\{(0,0), (0,1), (1,0)\} \end{aligned}

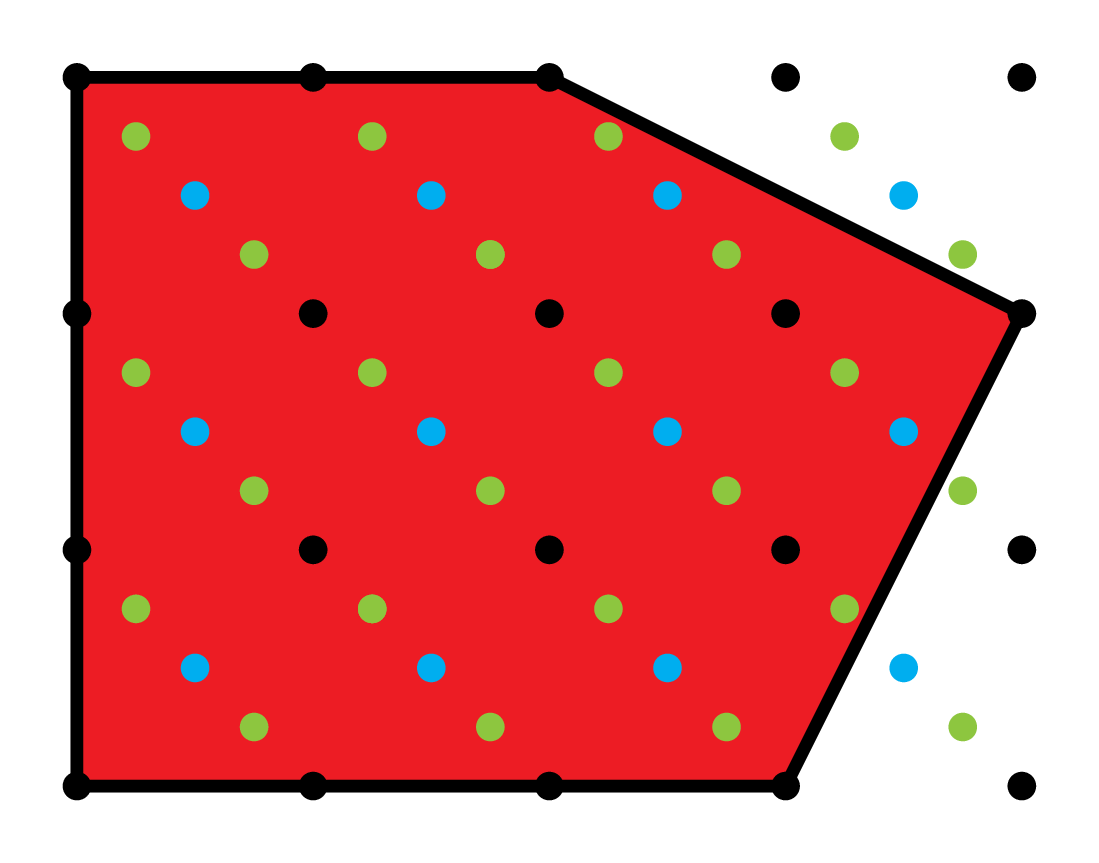
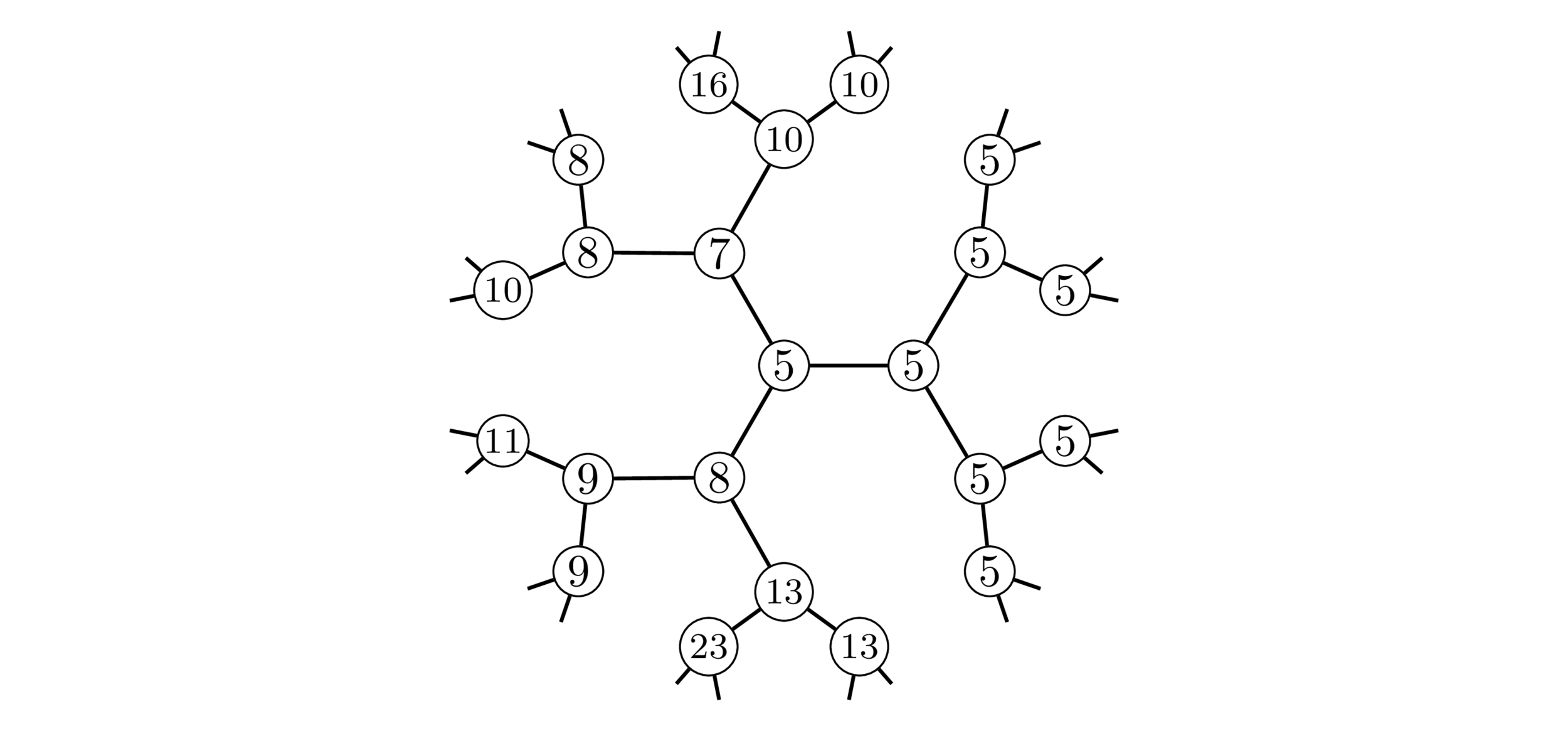
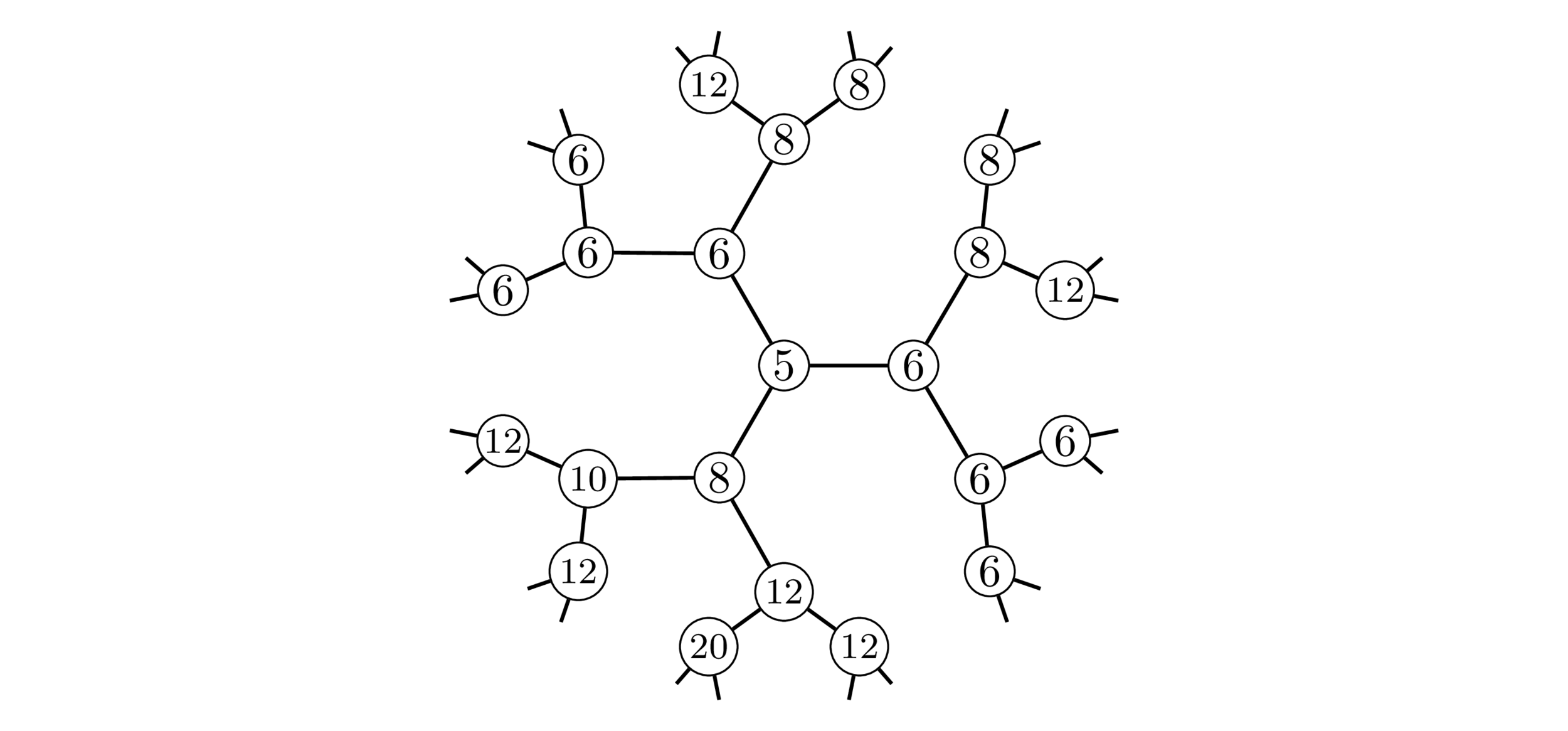
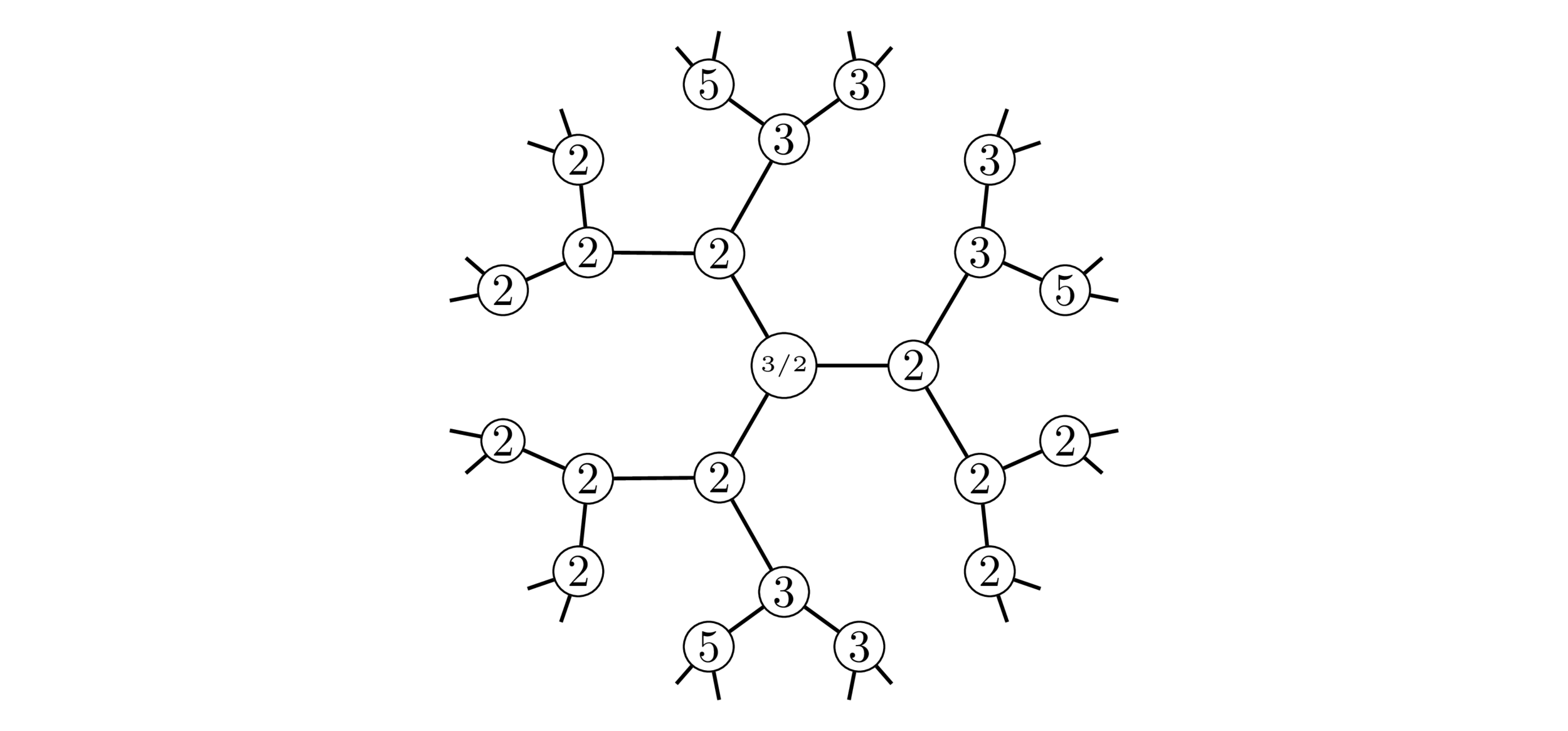
Normalized sums of coefficients

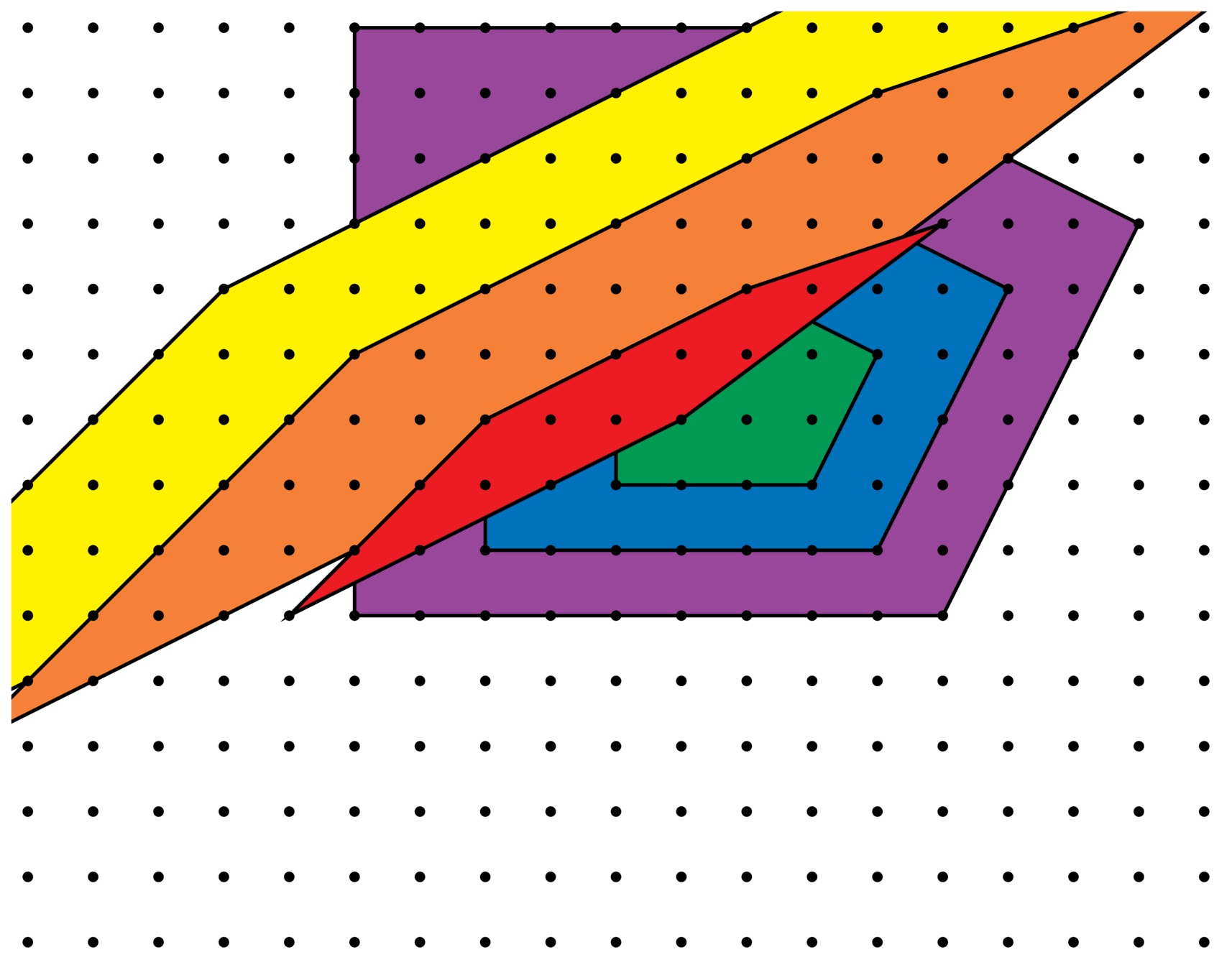
Fix a lattice $\Lambda_0=\mathbb{Z}^n$ and polytope $P$, with $\mathscr{E}_{n,\ell}^{\Lambda_0}(P)\neq 0$. Define

where $\Lambda\supseteq\Lambda_0$ runs over all lattices in $\mathbb{Q}^n$ with $\#(\Lambda/\Lambda_0)=m$.

Just as a lattice can be seen as a $\mathrm{GL}_n(\mathbb{Z})$-coset in $\mathrm{GL}_n(\mathbb{Q})\cap\mathrm{Mat}_n(\mathbb{Z})$,

a symplectic lattice is a $\mathrm{GSp}_{2n}(\mathbb{Z})$-coset in $\mathrm{GSp}_{2n}(\mathbb{Q})\cap\mathrm{Mat}_{2n}(\mathbb{Z})$.

\mathcal{C}_{P,\ell}^{\mathsf{A}} : \mathbb{N} \longrightarrow \mathbb{Q}

m \longmapsto \dfrac{1}{\mathscr{E}_{n,\ell}^{\Lambda_0}(P)} \sum_{\Lambda} \mathscr{E}_{n,\ell}^{\Lambda}(P),

Define $\mathcal{C}_{P,\ell}^{\mathsf{C}} : \mathbb{N}\to \mathbb{Q}$ similarly but restricted to symplectic lattices.

We computed $\mathcal{C}_{P,1}^{\mathsf{A}}(2)$ and $\mathcal{C}_{P,1}^{\mathsf{A}}(4)$.

An arithmetic function

Write $\mathsf{X}$ for either $\mathsf{A}$ or $\mathsf{C}$.

Proof uses Hecke algebra like in theory of automorphic forms.

Theorem (Alfes–M–Voll).

(Ind.) For polytopes $P$ and $P'$, with $\dim P=\dim P'$,

(Mult.) For $a,b\in \mathbb{N}$ with $\mathrm{gcd}(a,b)=1$,

\mathcal{C}_{P,\ell}^{\mathsf{X}}(ab) = \mathcal{C}_{P,\ell}^{\mathsf{X}}(a)\mathcal{C}_{P,\ell}^{\mathsf{X}}(b).

\mathcal{C}_{P,\ell}^{\mathsf{X}}=\mathcal{C}_{P',\ell}^{\mathsf{X}}.

Growth rate of coefficients

For functions $f,g : \mathbb{R}\to \mathbb{R}$, we write

f(N) \sim g(N) \quad \iff \quad \lim_{N\to \infty} \dfrac{f(N)}{g(N)} = 1.

Proposition (Alfes–M–Voll).

Let $\ell\in \{0,1,\dots, n\}$. Assuming $\mathscr{E}_{n,\ell}^{\Lambda_0}(P)\neq 0$,

\sum_{m=1}^{N} \mathcal{C}_{P,\ell}^{\mathsf{A}}(m) \,\sim\, \begin{cases} \frac{\zeta(n-\ell)}{n} \zeta(2)\zeta(3) \cdots \zeta(n-1) N^n & \text{if }\ell\leqslant n-2, \\[0.5em] \frac{1}{n}\zeta(2)\zeta(3) \cdots \zeta(n-2) N^n \log N & \text{if }\ell=n-1, \\[0.5em] \frac{1}{n+1} \zeta(2)\zeta(3) \cdots \zeta(n) N^{n+1} & \text{if }\ell=n. \end{cases}

Here, $\zeta$ is the Riemann zeta function.

Averaging over all lattices

Corollary.

Let $P$ be an $n$-dimensional polytope in $\Lambda_0$ and $\ell\in \{0,1,\dots, n-2\}$. The average $\ell$th Ehrhart coefficient of $P$, running over all $\Lambda\supseteq\Lambda_0$ in $\mathbb{Q}^n$ with finite co-index, approaches

\dfrac{\zeta(n-\ell)}{\zeta(n)} \mathscr{E}_{n,\ell}^{\Lambda_0}(P).

Example. For $n=3$, the average linear coefficient approaches

\dfrac{\pi^2}{6\zeta(3)}\mathscr{E}_{3,1}^{\Lambda_0}(P) \approx 1.37\cdot\mathscr{E}_{3,1}^{\Lambda_0}(P)

Example. For $n=4$, the average quadratic coefficient approaches

\dfrac{15}{\pi^2}\mathscr{E}_{4,2}^{\Lambda_0}(P) \approx 1.52\cdot \mathscr{E}_{4,2}^{\Lambda_0}(P)

Growth rate (symplectic edition)

Theorem (Alfes–M–Voll).

For each $\ell\in \{0,1,\dots, 2n\}$ there exists $c_{n,\ell}\in\mathbb{R}$ such that

\sum_{m=1}^{N}\mathcal{C}_{P,\ell}^{\mathsf{C}}(m) \,\sim\, c_{n,\ell}N^{\frac{n+1}{2} + \frac{1+\max(0,\ell-n)}{n}}(\log N)^{\delta_{n,\ell}}.

For $i,j\in\mathbb{N}_0$, write $\delta_{i,j}$ for the Kronecker delta symbol.

For $n=2$ (i.e. in $4$ dimensions) we completely know $c_{2,\ell}$:

\begin{aligned} c_{2,0} &= \frac{7\zeta(3)}{8}, & c_{2,1} &= \frac{\zeta(2)^2\zeta(3)}{12\zeta(5)}, & c_{2,2} &= \frac{5}{8}, & c_{2,3} &= \frac{2\zeta(2)^2\zeta(3)}{5\zeta(5)}, & c_{2,4} &= \frac{7\zeta(3)}{12}. \end{aligned}

Averaging over symplectic lattices

We do not know much about $c_{n,\ell}$, and hence averages over all symplectic lattices, for $n\geqslant 3$.

When $n=2$ and $\ell=1$, the average linear coefficient is

Corollary.

Let $P$ be $2n$-dimensional in $\Lambda_0$. The average $\ell$th Ehrhart coefficient, running over all symplectic lattices, converges only when $\ell\in\{0,1,\dots, n-1\}$. Its limit is

\dfrac{c_{n,\ell}}{c_{n,0}} \mathscr{E}_{2n,\ell}^{\Lambda_0}(P).

\dfrac{\pi^4}{63\zeta(5)}\mathscr{E}_{4,1}^{\Lambda_0}(P).

Quadratic permutation statistics

To understand the average Ehrhart coefficient over all symplectic lattices, we need to at least understand:

F_n(X) = \sum_{w\in S_n}X^{\mathrm{binv}(w) + \mathrm{des}(w)}.

(More specifically: $\prod_{p\text{ prime}} F_n(p^{-1})$.) The usual suspects:

\begin{aligned} \mathrm{Des}(w) &= \left\{i\in [n-1] ~\middle|~ w(i) > w(i+1) \right\} \\ \mathrm{des}(w) &= \# \mathrm{Des}(w) \\ \mathrm{inv}(w) &= \left\{(i,j) ~\middle|~ 1\leqslant i < j \leqslant n,\ w(i)> w(j) \right\} \end{aligned}

$\mathrm{binv}$ less studied, connections to lecture hall partitions Savage (2016)

\mathrm{binv}(w) = \mathrm{inv}(w) + \sum_{i\in \mathrm{Des}(w)} \binom{i + 1}{2}

The symplectic Hecke action

These results come from an action of the Hecke ring on the space of unimodular invariant valuations on polytopes.

is a basis for the space of unimodular invariant valuations $\mathrm{UIV}_{2n}$.

\left\{\mathscr{E}_{2n,0}^{\Lambda_0},\; \mathscr{E}_{2n,1}^{\Lambda_0},\; \dots,\; \mathscr{E}_{2n,2n}^{\Lambda_0}\right\}

By Betke–Kneser (1985), the set

An $\mathbb{R}$-valued function $\varphi$ on polytopes is a valuation if

\varphi(P) + \varphi(Q) = \varphi(P\cup Q) + \varphi(P\cap Q)

whenever $P, Q, P\cap Q, P\cup Q$ are polytopes.

A valuation $\varphi$ is unimodular invariant if for all $\alpha\in \mathrm{Aut}(\Lambda_0)\!\leqslant\! \mathrm{Aff}_{2n}(\mathbb{R})$

\varphi = \varphi\alpha.

\begin{aligned} G^+ &= \mathrm{GSp}_{2n}(\mathbb{Q}_p)\cap \mathrm{Mat}_{2n}(\mathbb{Z}_p), & \Gamma &= \mathrm{GSp}_{2n}(\mathbb{Z}_p) \end{aligned}

The (symplectic) Hecke ring $\mathcal{H}$ is the set of functions $G^+ \to \mathbb{Z}$ that:

are continuous (thus, locally constant),
have compact support,
are constant on $\Gamma$-double cosets.

$\mathbb{Z}$-basis for $\mathcal{H}$ : characteristic functions on $\Gamma$-double cosets.

\mathcal{H} = \mathbb{Z}[T_0, T_1, \dots, T_n].

\begin{aligned} D_0 &= \begin{pmatrix} I_n & \\ & pI_n \end{pmatrix}, & D_k &= \begin{pmatrix} I_{n-k} & & & \\ & pI_k & & \\ & & p^2I_{n-k} & \\ & & & pI_k \end{pmatrix}. \end{aligned}

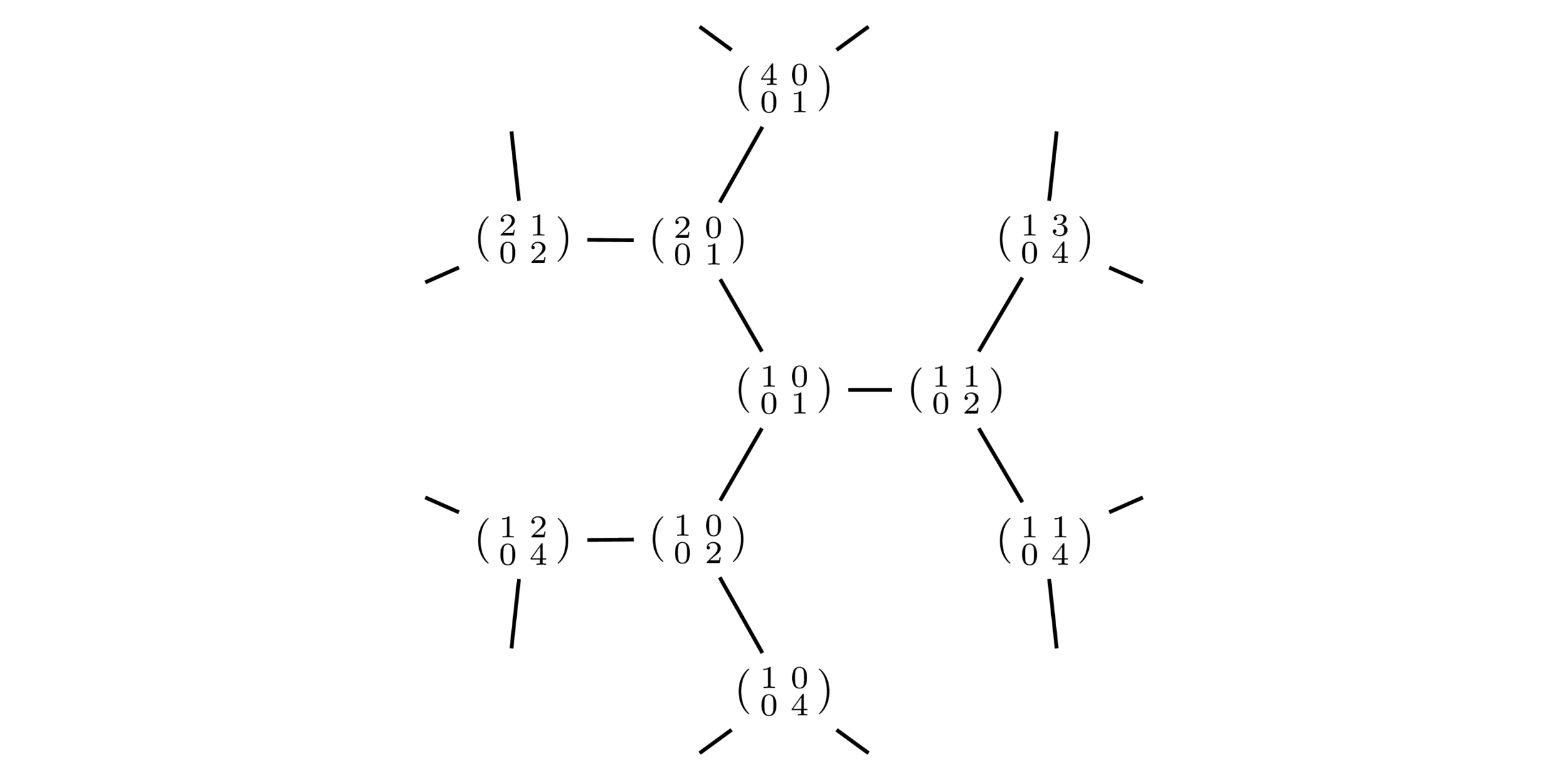
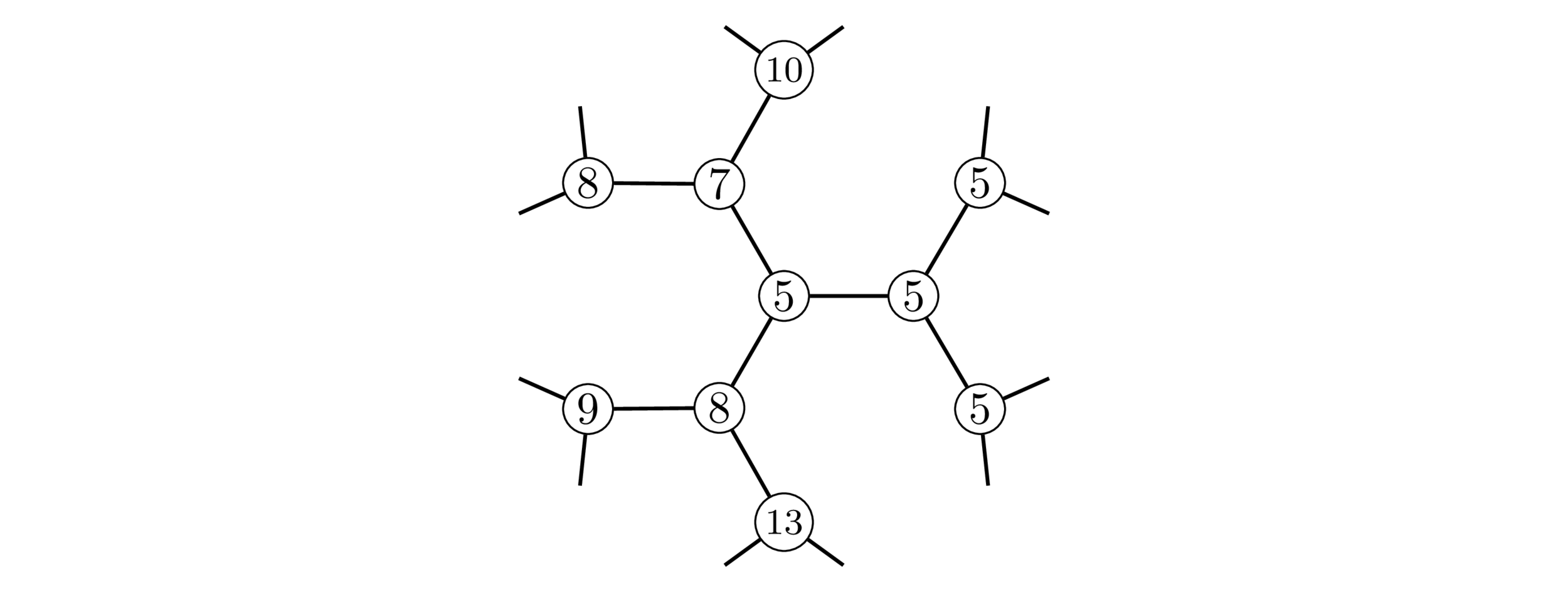
We define matrices $D_0,\dots, D_n\in G^+$: for $k\in \{1,\dots, n\}$,

Let $T_k\in\mathcal{H}$ be the characteristic function on $\Gamma D_k\Gamma$. By Krieg (1990),

For $f\in\mathrm{UIV}_{2n}$, define $Tf\in\mathrm{UIV}_{2n}$ via

where

$\Gamma\setminus \Gamma g \Gamma$ : set of left cosets whose union is $\Gamma g \Gamma$,

Extend linearly to define an action of $\mathcal{H}$ on $\mathrm{UIV}_{2n}$.

Let $T\in\mathcal{H}$ be the characteristic function for $\Gamma g\Gamma$.

What does this action look like on our generators $T_k$?

Tf(P) = \sum_{\Gamma h \,\in\, \Gamma \setminus \Gamma g\Gamma} f(h\cdot P)

$h\cdot P$ : given by some integer matrix in $\Gamma h$ acting on vertices.

Each matrix corresponds to a $\Gamma$-left coset.

Colors correspond to $\Gamma$-double cosets.

\Gamma\begin{pmatrix} 1 \\ &1 \\ &&p \\ &&&p \end{pmatrix}\Gamma

T_0

\Gamma\begin{pmatrix} 1 \\ &p \\ &&p^2 \\ &&&p \end{pmatrix}\Gamma

T_1

\Gamma\begin{pmatrix} p \\ &p \\ &&p \\ &&&p \end{pmatrix}\Gamma

T_2

Theorem (Alfes–M–Voll).

Let $k\in \{0,\dots, n\}$ and $\ell\in\{0, \dots, 2n\}$. There exist polynomials $\Phi_{n,k,\ell}(Y)\in\mathbb{Z}[Y]$ such that

T_k\mathscr{E}_{2n,\ell} = \Phi_{n,k,\ell}(p) \mathscr{E}_{2n,\ell}.

The polynomials satisfy

\dfrac{\Phi_{n,k,2n-\ell}^{\mathsf{C}}(Y)}{\Phi_{n,k,\ell}^{\mathsf{C}}(Y)} = \begin{cases} Y^{n-\ell} & \text{ if } k = 0, \\ Y^{2(n - \ell)} & \text{ if } k \in \{1,\dots, n\}. \end{cases}

Hecke eigenbases

Type $\mathsf{A}$ version was done by Gunnells and Rodrigeuz Villegas (2007).

The basis $\{\mathscr{E}_{2n,0},\dots,\mathscr{E}_{2n,2n}\}$ of $\mathrm{UIV}_{2n}$ is a simultaneous Hecke eigenbasis in types $\mathsf{A}$ and $\mathsf{C}$.

The Satake transform converts a Hecke operator to a polynomial.

Let $\Omega : \mathcal{H}\otimes \mathbb{Q} \to \mathbb{Q}[x_0,\dots, x_n]$ be the Satake transform and

From theory of spherical functions on $p$-adic groups, simultaneous Hecke eingenfunctions are in bijection with elements of $\mathbb{C}^{n+1}$.

\psi_{n,\ell} : \mathbb{Q}[x_0,\dots, x_n] \longrightarrow\mathbb{Q}\qquad x_i\longmapsto \begin{cases} p^{\ell} & \text{if }i=0, \\ p^{i} & \text{if }i\in \{1,\dots, n-1\}, \\ p^{n-\ell} & \text{if } i=n. \end{cases}

Theorem (Alfes–M–Voll).

Same hypotheses as previous theorem. For all primes $p$,

\Phi_{n,k,\ell}(p) = \psi_{n,\ell}(\Omega(T_k)).

Spherical parameters

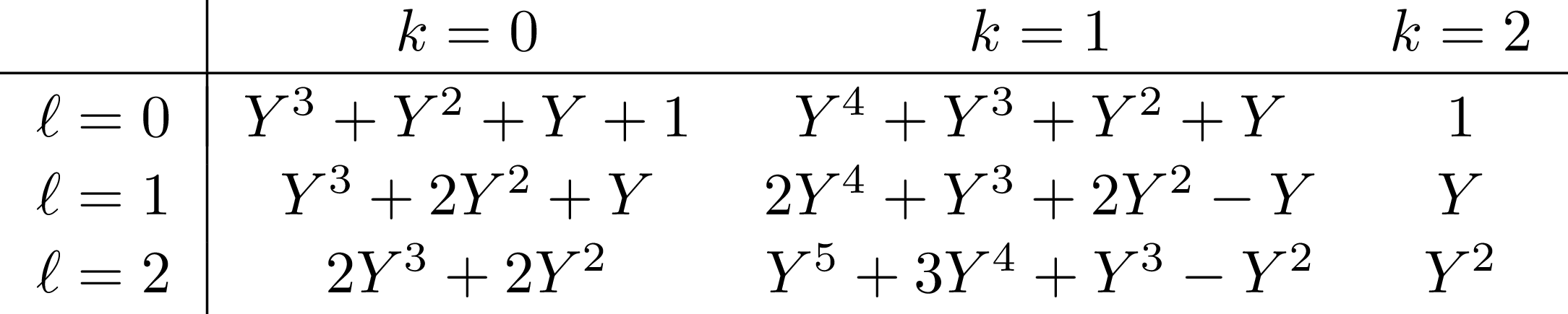
Explicit eigenvalues $\Phi_{n,k,\ell}(Y)$

$\Phi_{2, k, \ell}$

$\Phi_{3, k, \ell}$

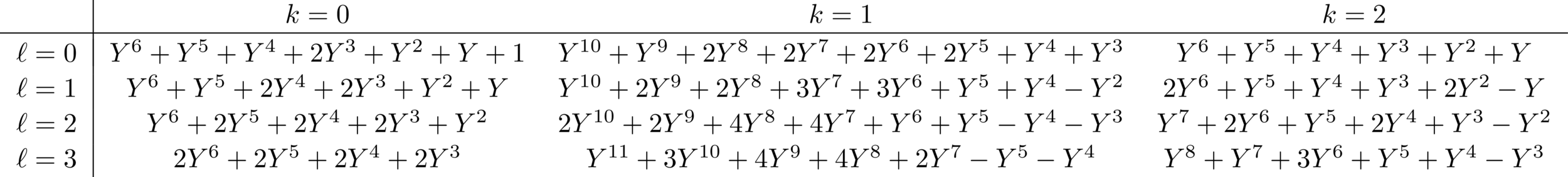
Knowing that the $\mathscr{E}_{2n,\ell}^{\Lambda_0}$ form a symplectic Hecke eigenbasis means we can take advantage of the theory of spherical functions.

There is a zeta function associated with the $\ell$th Ehrhart spherical parameters, $(p^{\ell}, p^1,\dots, p^{n-1},p^{n-\ell})$, as an integral over $G^+$.

We get a nice interpretation of that integral:

\mathcal{Z}_{n,\ell,p}^{\mathsf{X}}(s) = \sum_{\Gamma g \,\in\, \Gamma\setminus \Gamma G^+\Gamma} \dfrac{\mathscr{E}_{2n,\ell}(g\cdot P)}{\mathscr{E}_{2n,\ell}(P)} \left|\Lambda_{g} : \Lambda_0\right|^{-s}.

Ehrhart–Hecke zeta functions

Lattice

from $\Gamma g$

To understand growth of $\mathcal{C}_{P,\ell}^{\mathsf{X}}$, need to understand $\mathcal{Z}_{n,\ell,p}^{\mathsf{X}}$ for all $p$:

By Gunnells and Rodrigeuz Villegas (2007),

This follows from basic facts about symmetric functions and from work of Tamagawa after knowing the type $\mathsf{A}$ parameters:

(p^1, p^2, \dots, p^{n-1},p^{\ell})

\mathcal{Z}_{n,\ell}^{\mathsf{X}}(s) := \sum_{m=1}^{\infty} \mathcal{C}_{P,\ell}^{\mathsf{X}}(m)\, m^{-s} = \prod_{p\text{ prime}} \mathcal{Z}_{n,\ell,p}^{\mathsf{X}}(s)

\mathcal{Z}_{n,\ell}^{\mathsf{A}}(s) = \zeta(s - \ell) \cdot \zeta(s - 1) \zeta(s-2)\cdots \zeta(s - n + 1)

Lattice enumeration

Theory of spherical functions on $p$-adic groups gets us

$\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}$ as integral

over $G^+$

Hecke series at

$(p^{\ell},p^1,\dots, p^{n-1},p^{n-\ell})$

By applying M–Voll (2024), get 2 facts about $\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}$ via Hecke series:

Fact 1:

\left. \mathcal{Z}_{n,\ell,p}^{\mathsf{C}}(s) \right|_{p \rightarrow p^{-1}} = (-1)^{n+1} p^{n^2+\ell-2ns} \mathcal{Z}_{n,\ell,p}^{\mathsf{C}}(s)

Fact 2:

Formula for $\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}$ via enumerating lattices by Hermite and Smith normal forms simultaneously.

\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}(s) = \sum_{I,J\subseteq [n]} \Psi_{n,I,J}(p^{-1}) \prod_{i\in I} \dfrac{p^{\binom{i+1}{2} + i(n-i)}t^n}{1-p^{\binom{i+1}{2} + i(n-i)}t^n} \prod_{j\in J} \dfrac{p^{\binom{j+1}{2} + j(n-j) - n + \ell}t^n}{1-p^{\binom{j+1}{2} + j(n-j) - n + \ell}t^n}

Theorem (Alfes–M–Voll).

Setting $t = p^{-s}$,

More specifics about $\Psi_{n,I,J}(Y)\in \mathbb{Z}[Y]$ soon.

\Psi_{n,I,J}(Y) = \text{$Y$-multinomial coefficient} \times \prod (1 - Y^k)^{e_k}

Corollary.

For all $\ell\in \mathbb{Z}$,

\mathcal{Z}_{n,2n-\ell,p}^{\mathsf{C}}(s) = \mathcal{Z}_{n,\ell,p}^{\mathsf{C}}\left(s - \frac{n-\ell}{n}\right)

We observe remarkable symmetry about $\ell=n$:

For $n=2$, it's small enough to be about Riemann zeta functions:

\mathcal{Z}_{2,\ell}^{\mathsf{C}}(s) = \dfrac{\zeta(2s-2)\zeta(2s-3)\zeta(2s-\ell)\zeta(2s-\ell-1)}{\zeta(4s-\ell-2)}

We have lots of data on our

Zenodo repository

with examples up to $n=10$ including $\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}$ and $F_n$.

For $n\geqslant 3$, it is not so simple. Again, quadratic permutation statistics:

F_n(X) = \sum_{w\in S_n}X^{\mathrm{binv}(w) + \mathrm{des}(w)}

\mathcal{Z}_{n,0,p}^{\mathsf{C}}(s) = \dfrac{\displaystyle\sum_{w\in S_n}p^{-\mathrm{inv}(w)} \prod_{i\in\mathrm{Des}(w)} p^{\binom{n+1}{2} - \binom{i+1}{2}} t^n}{\displaystyle\prod_{i=0}^n\left(1 - p^{\binom{n+1}{2} - \binom{i+1}{2}}t^n\right)}

Proposition. ($\ell=0$):

\mathcal{Z}_{n,n,p}^{\mathsf{C}}(s) = \dfrac{\displaystyle\sum_{w\in S_n}p^{-\mathrm{inv}(w)} \prod_{i\in\mathrm{Des}(w)} p^{\binom{n+1}{2} - \binom{i}{2}} t^n}{\displaystyle\prod_{i=1}^{n+1}\left(1 - p^{\binom{n+1}{2} - \binom{i}{2}}t^n\right)}

Conjecture. ($\ell=n$):

\begin{aligned} \mathcal{Z}_{3, 0, p}^{\mathsf{C}}(s) &= \dfrac{1 + pt^3 + p^2t^3 + p^3t^3 + p^4t^3 + p^5t^6}{(1 - t^3)(1 - p^3t^3)(1 - p^5t^3)(1 - p^6t^3)} \\[2.5em] \mathcal{Z}_{3, 1, p}^{\mathsf{C}}(s) &= \dfrac{1 + p^2t^3 + p^4t^3 - p^4t^6 - 2p^5t^6 - 2p^7t^6 - p^8t^6 + p^8t^9 + p^{10}t^9 + p^{12}t^{12}}{(1 - pt^3)(1 - p^3t^3)^2(1 - p^4t^3)(1 - p^5t^3)(1 - p^6t^3)} \\[2.5em] \mathcal{Z}_{3, 2, p}^{\mathsf{C}}(s) &= \dfrac{1 + p^3t^3 + p^4t^3 - p^5t^6 - 2p^6t^6 - 2p^8t^6 - p^9t^6 + p^{10}t^9 + p^{11}t^9 + p^{14}t^{12}}{(1 - p^2t^3)(1 - p^3t^3)(1 - p^4t^3)(1 - p^5t^3)^2(1 - p^6t^3)} \\[2.5em] \mathcal{Z}_{3, 3, p}^{\mathsf{C}}(s) &= \dfrac{1 + p^3t^3 + 2p^4t^3 + p^5t^3 + p^8t^6}{(1 - p^3t^3)(1 - p^5t^3)(1 - p^6t^3)^2} \end{aligned}

Idea of proof for formula

Fix a partition $\lambda$, with at most $n$ parts, and composition $\delta\in \mathbb{N}_0^n$.

Lattices $\Lambda\subseteq\Lambda_0=\mathbb{Z}_p^n$ with

\begin{aligned} \mathrm{htimS}(\Lambda) &= \begin{pmatrix} p^{\lambda_1} \\ & p^{\lambda_2} \\ & & \ddots \\ & & & p^{\lambda_{n-1}} \\ & & & & p^{\lambda_n} \end{pmatrix}, & \mathrm{Hermite}(\Lambda) &= \begin{pmatrix} p^{\delta_1} & * & & \dots & *\\ & p^{\delta_2} & * & \dots & * \\ & & \ddots & \ddots & \vdots \\ & & & p^{\delta_{n-1}} & * \\ & & & & p^{\delta_n} \end{pmatrix} \end{aligned}

are determined by semi-standard Young tableaux of shape $\lambda$ and weight $\delta$.

Because of spherical parameters, need only fix $\lambda$ and $\delta_n$.

In other words, we need a partition $\lambda$ and a horizontal strip.

Fix rank one lattice $L\subset\Lambda_0$. Let $\pi : \Lambda_0 \twoheadrightarrow \Lambda_0/L$. Want $\Lambda\subseteq \Lambda_0$ such that

\mathrm{type}(\Lambda_0/\Lambda)=\lambda \qquad \#\Lambda\cap L = p^{\delta_n}

Let $\mu$ be the type of $\pi(\Lambda)$, so $\lambda - \mu$ is a horizontal strip, call it $\sigma$.

I = \{4, 2\}

J = \{5, 2,1\}

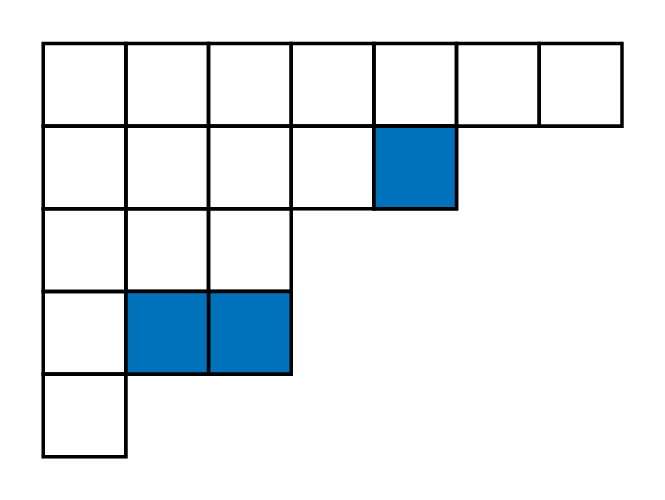
Define sets $I,J\subseteq \{1,\dots, n\}$ via

$I$ : column lengths containing $\sigma$

$J$ : column lengths avoiding $\sigma$

p^{e(I, J, m_I, m_J)}\Psi_{n,I,J}(p^{-1}).

For multiplicities $m_I\in \mathbb{N}^I$ and $m_J\in\mathbb{N}^J$, number of such lattices is

The rest is just geometric progressions 🤙

Summary

The $\mathscr{E}_{2n,\ell}$ form a symplectic Hecke eigenbasis of $\mathrm{UIV}_{2n}$.

Theory of spherical functions on $p$-adic groups provide tools to study growth of coefficients.

The average $\ell$th coefficient of the Ehrhart polynomial...

is $\zeta(n-\ell)/\zeta(n)$ for $\ell\in\{0,\dots, n-2\}$ over all lattices,
converges for $\ell\in \{0,\dots, 2n/2 - 1\}$ over sympletic lattices.

Converted problem to lattice enumeration to get $\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}$ explicitly.

Two functional equations!
And evidence for special $\ell$-value: $\ell=n$.

Symplectic Hecke eigenbases from Ehrhart polynomials

Ehrhart polynomials

Lattices

Normalized sums of coefficients

An arithmetic function

Growth rate of coefficients

Averaging over all lattices

Growth rate (symplectic edition)

Averaging over symplectic lattices

Quadratic permutation statistics

The symplectic Hecke action

Hecke eigenbases

Spherical parameters

Explicit eigenvalues \(\Phi_{n,k,\ell}(Y)\)

Ehrhart–Hecke zeta functions

Lattice enumeration

Idea of proof for formula

Summary

Thank you!