Igusa zeta functions and hyperplane arrangements
How to Navigate:
Spacebar: Forward
Shift + Spacebar: Backward
Escape: Jump around
Arrow keys: Move around
The Igusa zeta function
Let \(f\in \mathbb{Z}[x_1, \dots, x_d]\). For every positive integer \(n\):
- Can we write a formula for \(R(n)\)?
If \(n = p_1^{e_1} \cdots p_{\ell}^{e_{\ell}}\) is the prime factorization of \(n\), then
So we focus on a prime \(p\).
- How does \(R(p_i^{e_i})\) vary as \(i\) varies?
- How does \(R(n)\) grow as \(n\) grows?
- Only finitely many different formulae for the \(R(p^e)\) over all primes \(p\)?
We focus on polynomials equal to product of linear factors.
Leading terms!
Theorem (Igusa 1974).
- The \(R(p^e)\) grow like a polynomial,
- only finitely many different formulae for \(R(p^e)\), and
- there is a finite linear recurrence relation among \(R(p^{e_i})\).
Example.


- \(p >2\)
- \(p =2\)
Overview
Understand features of Igusa zeta function with combinatorial & topological tools
flag Hilbert–Poincaré series
Igusa zeta function
combinatorial "coarsening"
Define flag Hilbert–Poincaré series and give substitution.
Hyperplane arrangements
Hyperplane arrangement \(\mathcal{A}\) finite set of hyperplanes in \(K^d\).
Intersection poset: ordered by reverse inclusion
- Bottom element \(\hat{0}\) : the vector space \(K^d\).
- Top element \(\hat{1}\) : the common intersection (if exists).
If \(\hat{1}\in\mathcal{L}(\mathcal{A})\), then \(\mathcal{A}\) is central.


Poincaré polynomial:
Coefficients are Betti numbers.
Example.
\(\mathrm{codim}\)
0
1
2
3
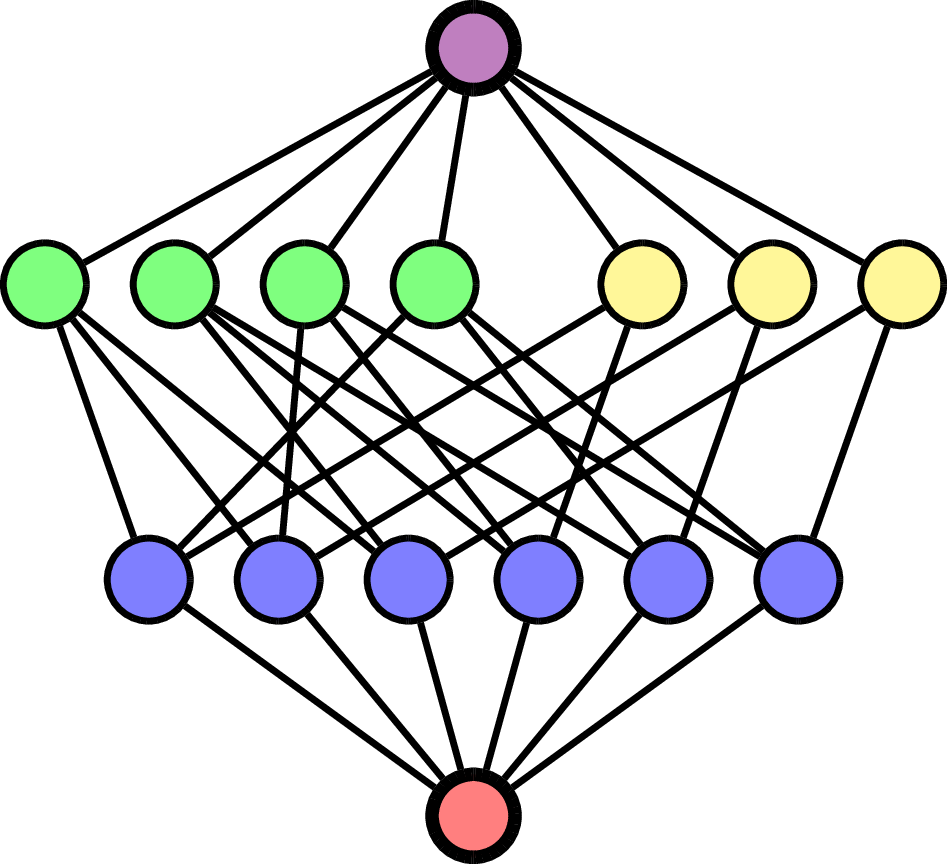
\(\mathcal{L}(\mathsf{A}_3)\)
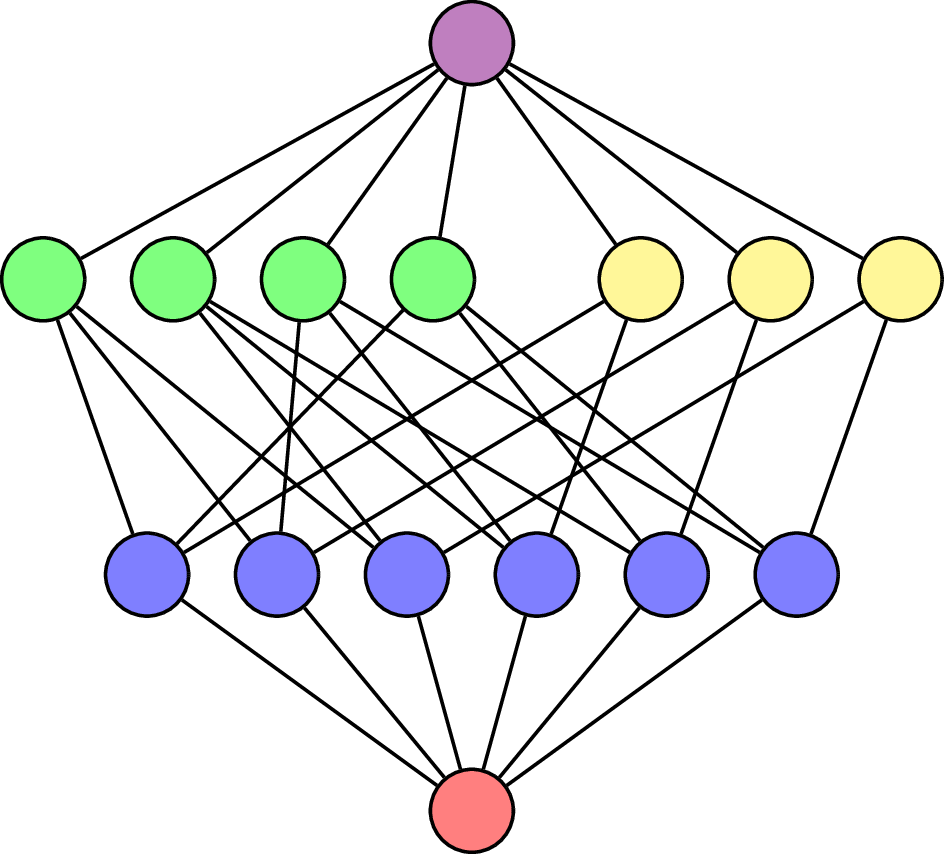
\(\hat{0}\)
\(\hat{1}\)

\(\mathsf{A}_3\)
\(K\!=\!\mathbb{C}\)
Write \(\Delta(\mathcal{L}(\mathcal{A})\setminus \{\hat{0}\})\) for flags of proper subspaces in \(\mathcal{L}(\mathcal{A})\).
For flag \(F = (F_1< \cdots <F_{\ell}) \in \Delta(\mathcal{L}(\mathcal{A})\setminus \{\hat{0}\})\), generalize:
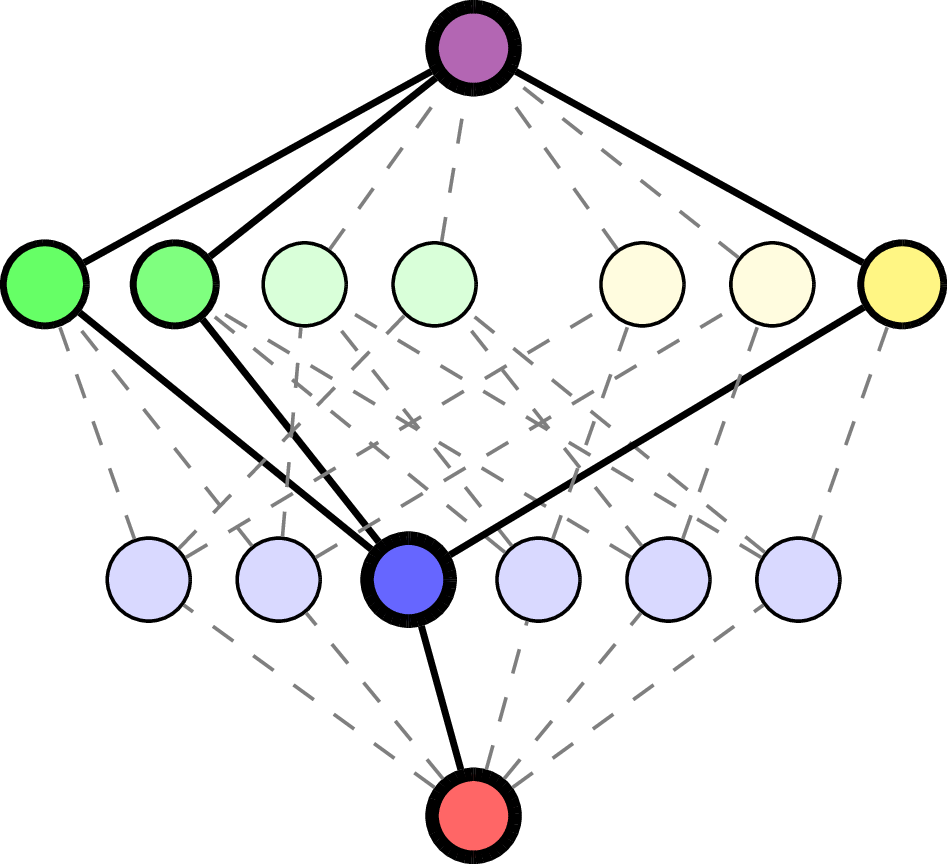
Example.
\(F = (\quad\;)\):

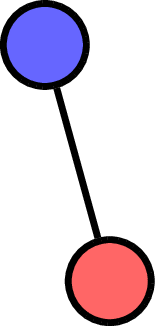





Self reciprocity
The flag Hilbert–Poincaré series:
Idea: \(\mathsf{fHP}_{\mathcal{A}}\) is equivalent to a multivariate \(p\)-adic integral.
Theorem (M., Voll 2024). For \(\mathcal{A}\) defined over field of characteristic \(0\) and central, then
For \(x\in\mathcal{L}(\mathcal{A})\), set
All potential poles come from combinatorial data:
Back to Igusa zeta functions
is the Igusa zeta function associated to \(\mathcal{A}\).
Theorem (M., Voll 2024). If \(\mathcal{A}\) defined over \(\mathbb{Q}\), then for all but finitely many primes \(p\),
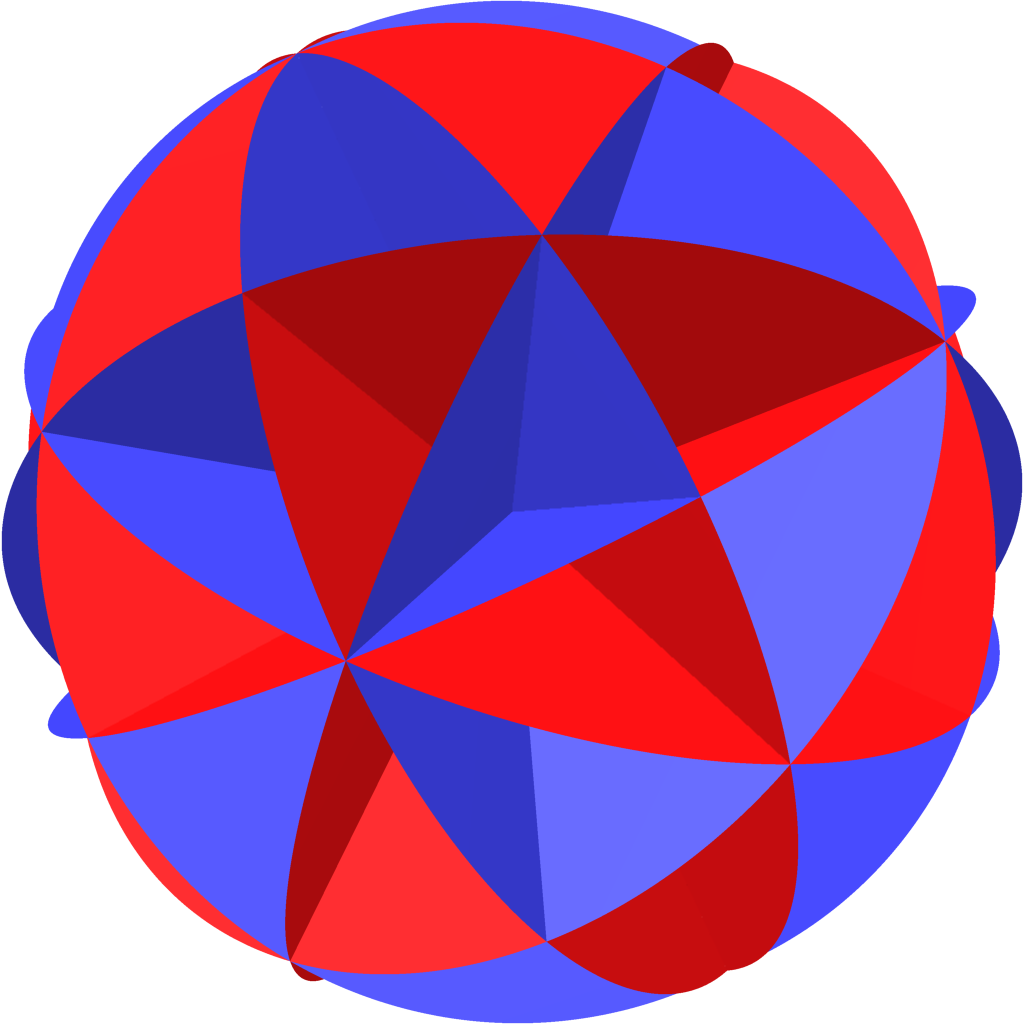
Example.
Back to our original data:
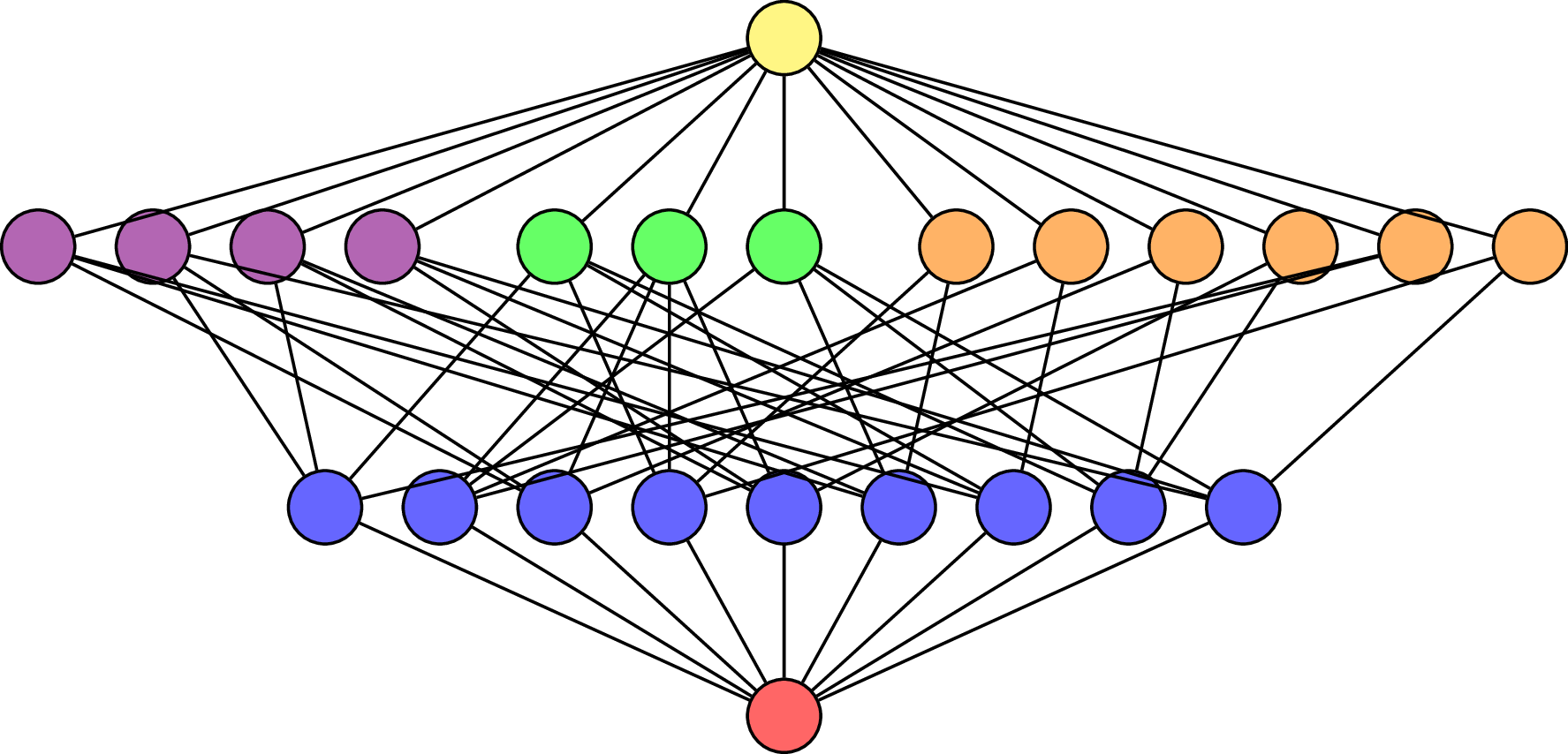
\(\mathcal{L}(\mathsf{B}_3)\)





A different coarsening
Set each \(T_x=T\) — coarse flag Hilbert–Poincaré series:
Nice form:
of \(\mathcal{L}(\mathcal{A})\)
codim of
maximal elt
Corollary. For every hyperplane arrangement \(\mathcal{A}\), the coefficients of \(\mathcal{N}_{\mathcal{A}}(Y, T)\) are non-negative.
Theorem (Dorpalen-Barry, M., Stump +2023). The coefficients of \(\mathcal{N}_{\mathcal{A}}(Y, T)\) count
together with two statistics on the pair.
Numerator polynomial looks something like:
Summary
- Combinatorially defined substitution from flag Hilbert–Poincaré series to Igusa zeta function.
- Self-reciprocity of flag Hilbert–Poincaré series yield palindromicity of coefficients.
- Coefficients of numerator of coarse flag Hilbert–Poincaré series are non-negative.
flag Hilbert–Poincaré series
Igusa zeta function
combinatorial "coarsening"
