An alternate proof to Birkhoff's formula

Contents

• The formula
• The proof
• An example
• References

We give an alternate proof of a formula due to Birkhoff [1, Thm. 8.1] counting the number of subgroups of type $\nu$ contained in an abelian $p$-group of type $\lambda$, where $\lambda$ and $\nu$ are partitions. A more modern version of Birkhoff’s theorem can be found in Butler [2, Thm. 1.6.1]; she also fixed many typographical errors in Birkhoff’s statement and adds additional explanation. Butler [2] is a fantastic manuscript on enumeration in group theory.

The formula

Birkhoff’s formula uses notation related to partitions and Young diagrams. Let $\lambda = (\lambda_1,\lambda_2,\dots )$ be a partition (so all but finitely many $\lambda_i$ are $0$), and we always assume $\lambda_i\geqslant \lambda_{i+1}$. One of the many ways a partition $\lambda$ can be visualized is via Young diagrams. The Young diagram of shape $\lambda$ has $\lambda_i$ boxes in row $i$ while aligning to the left. We refer to parts of the Young diagram like we would a matrix: it has an $i$th row, a $j$th column, and a box in the $(i,j)$-entry.

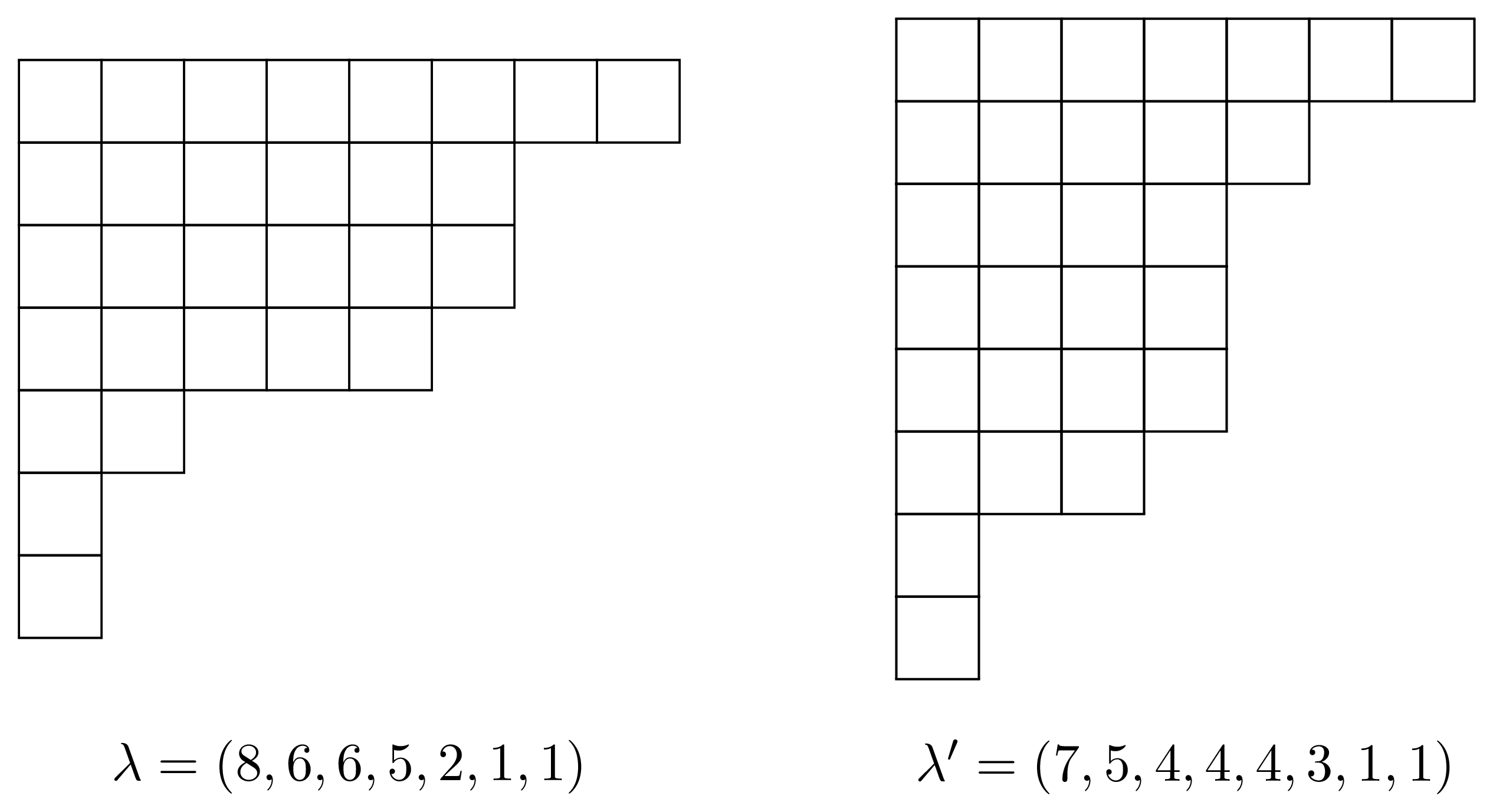
Figure 1. A Young diagram and its conjugate.

Throughout $p$ is a fixed prime, and $G$ is a finite abelian $p$-group whose operation we denote by $+$. An abelian $p$-group of type $\lambda$ is isomorphic to \[ C_p(\lambda) = \prod_{i\geqslant 1} \mathbb{Z}/p^{\lambda_i}\mathbb{Z} . \]

We will also need the Gaussian binomial coefficients. In a different post, we described Schubert cells, which are not necessary here, but they interesting and related.

Now we can state Birkhoff’s formula.

Theorem 1. The number of subgroups of type $\nu$ in $C_p(\lambda)$ is \[ \prod_{i\geqslant 1} p^{\nu_{i+1}^{\prime} (\lambda_i^{\prime} - \nu_i^{\prime})} \binom{\lambda_i^{\prime} - \nu_{i+1}^{\prime}}{\nu_i^{\prime}-\nu_{i+1}^{\prime}}_p . \]

Birkhoff’s proof works by constructing a unique “standard matrix” for all subgroups in an abelian $p$-group. I want a proof that would avoid writing elements in a standard form, and one that I could look at two Young diagrams and “see” the answer. Also since there is a Gaussian binomial coefficient, I consider it a bonus if we relate this to $\mathbb{F}_p$-vector spaces.

The proof

We a few definitions from group theory. We assume throught that $G$ is a finite $p$-group. For $i\geqslant 0$, the $i$th Omega subgroup of $G$ is \[ \Omega_i(G) = \left\langle x \in G ~\middle|~ p^ix = 0 \right\rangle . \] The exponent of $G$ is the smallest integer $e\geqslant 0$ such that for all $g\in G$, we have $p^eg=0$.

Let $G$ be of type $\lambda$, and write $\Omega_i = \Omega_i(G)$. Let $V_i = \Omega_i/\Omega_{i-1}$ for all $i\geqslant 1$. Therefore, $V_i$ is an $\F_p$ vector space, and $\dim(V_i)=\lambda_i^{\prime}$. Our proof works via induction down the (ascending) $\Omega$-series. Essentially, we select suitable subspaces in various $V_i$; bases for such subspaces yield a set of generators for a subgroup $H$ of type $\nu$.

Since the exponent of $G$ is $e= \lambda_1$, let $U_e\leqslant V_e$ be a $\nu_e^{\prime}$-dimensional subspace. There is exactly one subgroup of $G/\Omega_{e-1}$, call it $\overline{H}_e$, such that $\overline{H}_e = U_e$.

Suppose we have a subspace $U_{i+1}$ in $V_{i+1}$. We set \[ pU_{i+1} = \left\langle \,px + \Omega_{i-1} ~\middle|~ x + \Omega_{i} \in U_{i+1} \right\rangle \leqslant V_i . \] Choose a $(\nu_i^{\prime} - \nu_{i+1}^{\prime})$-dimensional subspace, $U_i/pU_{i+1}$, inside a $(\lambda_i^{\prime} - \nu_{i+1}^{\prime})$-dimensional vector space, $V_i/pU_{i+1}$. The number of such subspaces is \[ \binom{\lambda_i^{\prime} - \nu_{i+1}^{\prime}}{\nu_i^{\prime} - \nu_{i+1}^{\prime}}_p . \] Let $U_i\leqslant V_i$ be the pre-image of the chosen subspace together with $pU_{i+1}$.

We assume we have a collection of $\F_p$-vector spaces $\mathcal{U}=\{U_i ~|~ i\geqslant 1\}$. To count the number of subgroups of $G$ coming from $\mathcal{U}$, we build such a subgroup inductively and count the number of distinct choices along the way. To start, let $H_e \leqslant G$ such that $\Omega_{e-1}\leqslant H_e$ and $U_e = H_e/\Omega_{e-1}$; there is exactly one choice for such an $H_e$, and $H_e$ has rank $\nu_e^{\prime}$. Now suppose we have such a subgroup $H_k\leqslant G$, and we want to construct $H_{k-1}\leqslant G$ such that $\Omega_{k-2}\leqslant H_{k-1}$, \[ \begin{aligned} H_k/\Omega_{k-1} &= H_{k-1}\Omega_{k-1}/\Omega_{k-1}, & &\text{and} & \Omega_{1}(H_{k-1})\Omega_{k-2}/\Omega_{k-2} &= U_{k-1}. \end{aligned} \] The number of such subgroups $H_{k-1}$ is determined by lifting a minimal generating set of $H_k/\Omega_{k-1}$ to $G/\Omega_{k-2}$. For each possible choice of lift, there are $p^{\nu_{k-1}^{\prime}}=\# U_{k-1}$ choices yielding the same group $H_{k-1}$. Since there are $p^{\lambda_{k-1}^{\prime}} = \# V_{k-1}$ choices in total, it follows that there are $p^{\lambda_{k-1}^{\prime}-\nu_{k-1}^{\prime}}$ distinct subgroups $H_{k-1}$ for a given subgroup $H_k$.

We have a chain of subgroups \[ H_e \geqslant H_{e-1} \geqslant \cdots \geqslant H_1 =: H. \] For each $i\in [e]$, the rank of $H_i$ is $\nu_i^{\prime}$ and the type is \[ \left(\min(\nu_j-i+1, 0)\right)_{j\geqslant 1} \] Therefore, $H$ is a subgroup of type $\nu$, and the statement of Theorem 1 follows.

An example

We illustrate the ideas from The proof here. Suppose we have two partitions:

\[ \begin{aligned} \lambda &= (8, 8, 5, 5, 5, 3, 1, 1), & \nu &= (4, 4, 4, 4, 2, 2, 1, 0). \end{aligned} \]

Figure 2 illustrates the two Young diagrams for $\lambda^{\prime}$ and $\nu^{\prime}$.

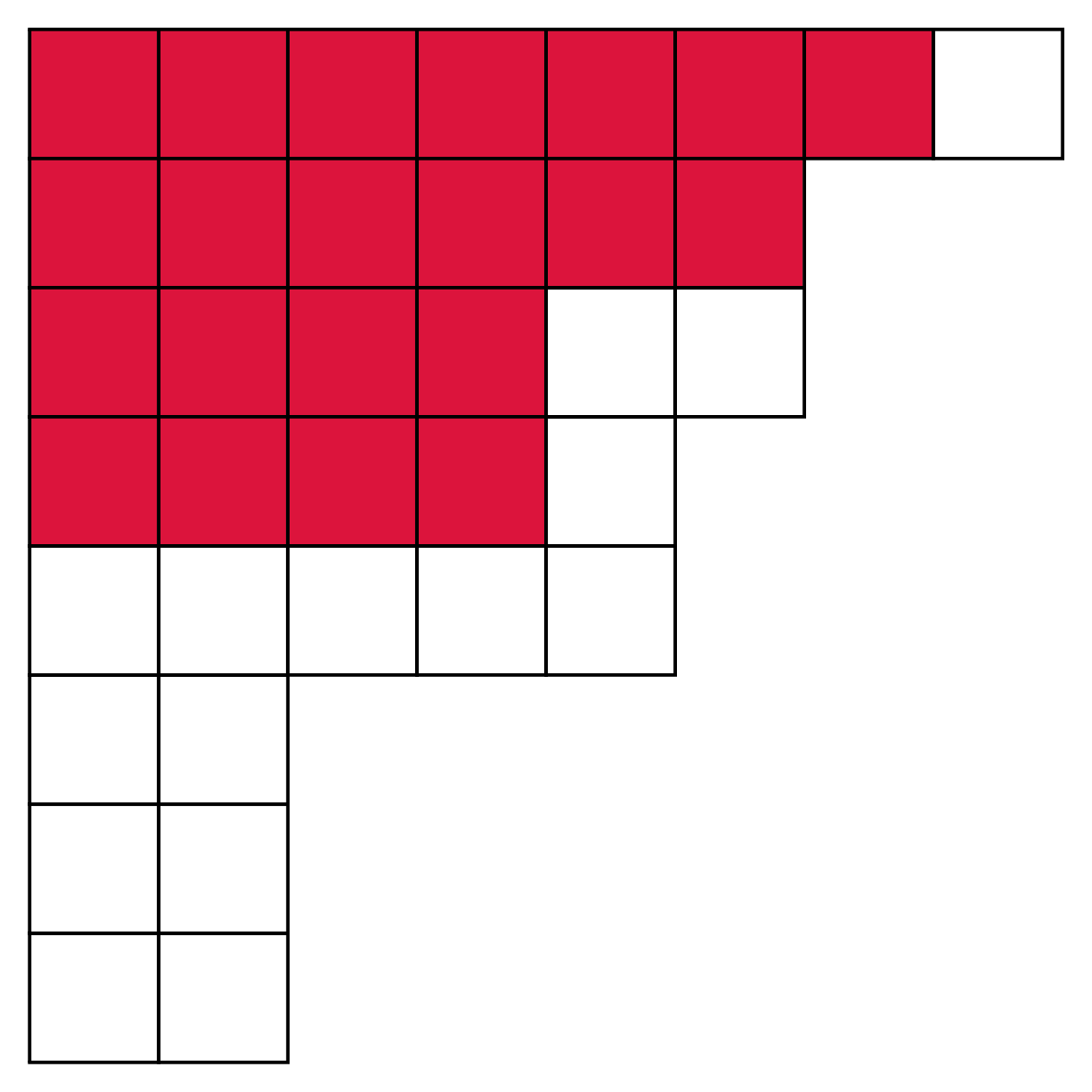
Figure 2. The Young diagram for $\lambda^{\prime}$ with the Young diagram for $\nu^{\prime}$ super-imposed and filled in red.

The subspaces $V_i$ and $U_i$ have dimensions given in the following table

$i$	1	2	3	4	5	6	7	8
$\dim(V_i)$	2	2	2	5	5	6	6	8
$\dim(U_i)$	0	0	0	0	4	4	6	7

Therefore, the number of subgroups of $C_p(\lambda)$ with type $C_p(\nu)$ is equal to \[ \binom{5}{4}_p \binom{2}{1}_p p^{8+6} = p^{14}(p^4 + p^3 + p^2 + p + 1)(p + 1) \in O(p^{19}). \]

References

[1] Garrett Birkhoff, Subgroups of Abelian Groups, Proc. London Math. Soc. (2) 38 (1935), 385–401.

[2] Lynn M. Butler, Subgroup lattices and symmetric functions, Mem. Amer. Math. Soc. 112 (1994), no. 539, vi+160.

---